37.计算几何入门

发表于 分类于 ，

计算几何入门

初高中解析几何关注理论求解，通过代数方法研究几何性质。算法竞赛中的计算几何则面临实际计算问题：

  1. 数值精度：浮点数运算存在误差，简单几何判断可能因精度问题失败
  2. 算法实现：将几何概念转化为可编程的算法步骤
  3. 避免除法：解析几何大量使用除法，而在计算机的浮点运算中，除法损失精度严重，计算几何的精髓在于尽可能用乘法代替除法，避免精度损失。

点积与叉积、点线关系、多边形与简单多边形、简单多边形面积、凸包、半平面交。

点积与叉积

为什么学点积与叉积？

点积和叉积是计算几何的基础工具，几乎所有几何问题都离不开它们：

  • 点积：判断向量夹角、投影长度、距离计算
  • 叉积：判断方向、计算面积、判断点线关系

解析几何中判断点线关系需要除法（如斜率比较），而计算几何用叉积的符号判断，完全避免除法运算。

点积（Dot Product）

定义：\(\vec{a} \cdot \vec{b} = |a||b|\cos\theta = a_x b_x + a_y b_y\)

公式推导：

设 \(\vec{a} = (a_x, a_y)\)，\(\vec{b} = (b_x, b_y)\)，夹角为 \(\theta\)。

为什么 \(a_x b_x + a_y b_y = |a||b|\cos\theta\)？

\(\vec{a} \cdot \vec{b} =|a||b|\cos\theta\) 的推导：

  • 直接计算：\(\vec{a} \cdot \vec{b} = a_x b_x + a_y b_y\)
  • 利用余弦定理：\(|\vec{a} - \vec{b}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2|\vec{a}||\vec{b}|\cos\theta\)
  • 展开左边：\(|\vec{a} - \vec{b}|^2 = (a_x - b_x)^2 + (a_y - b_y)^2 = a_x^2 + a_y^2 + b_x^2 + b_y^2 - 2(a_x b_x + a_y b_y)\)
  • 对比得到：\(a_x b_x + a_y b_y = |a||b|\cos\theta\)

\(\vec{a} \cdot \vec{b}=a_x b_x + a_y b_y\) 的推导：

  • 在直角坐标系中，\(x\) 轴和 \(y\) 轴是垂直的，所以 \(\vec{i} \cdot \vec{i} = 1\)，\(\vec{j} \cdot \vec{j} = 1\)，\(\vec{i} \cdot \vec{j} = 0\)
  • 向量 \(\vec{a} = a_x \vec{i} + a_y \vec{j}\)，\(\vec{b} = b_x \vec{i} + b_y \vec{j}\)
  • 利用点积的分配律：\(\vec{a} \cdot \vec{b} = (a_x \vec{i} + a_y \vec{j}) \cdot (b_x \vec{i} + b_y \vec{j}) = a_x b_x + a_y b_y\)

直观理解：点积就是两个向量对应坐标相乘再相加，结果等于长度乘以夹角的余弦。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct Point {
    double x, y;
    Point(double a, double b) {x = a, y = b;}
    
    // 点积：a·b = ax*bx + ay*by
    inline double dot(const Point &b) const {
        return x * b.x + y * b.y;
    }
    
    // 距离：|a-b| = sqrt((a-b)·(a-b))
    inline double Dis(const Point &b) const {
        return sqrt((*this - b).dot(*this - b));
    }
};

叉积（Cross Product）

定义：\(\vec{a} \times \vec{b}\) 是一个向量，方向垂直于 \(\vec{a}\) 和 \(\vec{b}\) 所在平面，大小等于以这两个向量为邻边的平行四边形的面积。在二维平面中，叉积方向垂直于平面，用正负号表示方向：当 \(\vec{b}\) 在 \(\vec{a}\) 的逆时针方向时，叉积为正；当 \(\vec{b}\) 在 \(\vec{a}\) 的顺时针方向时，叉积为负。

正负判断（右手定则）：右手四指从 \(\vec{a}\) 的方向弯向 \(\vec{b}\) 的方向，大拇指指向的方向就是叉积的方向。如果大拇指指向屏幕外（靠近观察者），则叉积为正；如果指向屏幕内（远离观察者），则叉积为负。

\(\vec{a} \times \vec{b} = |a||b|\sin\theta = a_x b_y - a_y b_x\)

\(\vec{a} \times \vec{b} = |a||b|\sin\theta\) 的推导：

  • 平行四边形面积 = 底 × 高 = \(|a| \times (|b|\sin\theta) = |a||b|\sin\theta\)

\(\vec{a} \times \vec{b} = a_x b_y - a_y b_x\) 的推导：

  • 在直角坐标系中，\(\vec{i} \times \vec{i} = 0\)，\(\vec{j} \times \vec{j} = 0\)，\(\vec{i} \times \vec{j} = 1\)，\(\vec{j} \times \vec{i} = -1\)
  • 向量 \(\vec{a} = a_x \vec{i} + a_y \vec{j}\)，\(\vec{b} = b_x \vec{i} + b_y \vec{j}\)
  • 利用叉积的分配律：\(\vec{a} \times \vec{b} = (a_x \vec{i} + a_y \vec{j}) \times (b_x \vec{i} + b_y \vec{j}) = a_x b_y - a_y b_x\)
1
2
3
4
5
6
struct Point {
    // 叉积：a×b = ax*by - ay*bx
    inline double cross(const Point &b, const Point &c) const {
        return (b.x - x) * (c.y - y) - (c.x - x) * (b.y - y);
    }
};

点线关系

浮点精度与 dcmp

计算几何中大量使用浮点数，直接比较浮点数是否相等容易出错。常用技巧是设定一个极小的正数 \(\varepsilon\)（eps），用 dcmp 函数判断浮点数的正负和是否接近零：

1
2
3
4
5
const double eps = 1e-8;
int dcmp(double x) {
    if(fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}

  • \(|x| < \varepsilon\) 视为 \(x=0\)

  • \(x > \varepsilon\) 视为正，\(x < -\varepsilon\) 视为负

  • 这样可以有效避免浮点误差带来的判断错误

角度与弧度

  • 角度：常用单位，360°为一圈

  • 弧度：数学和计算几何中常用，\(2\pi\)（大约6.28）为一圈

  • 换算：\(1\text{弧度} = 180/\pi\text{度}\)，\(1\text{度} = \pi/180\text{弧度}\)

  • 注意：计算几何中所有三角函数、旋转等都用弧度

三点共线

三点\(A,B,C\)共线，当且仅当\(\overrightarrow{AB}\)和\(\overrightarrow{AC}\)平行。用叉积判断：

  • \(\overrightarrow{AB} \times \overrightarrow{AC} = 0\) 时三点共线。

  • 叉积为零说明两个向量方向一致或相反。

  • 直观理解：\(|\overrightarrow{AB} \times \overrightarrow{AC}| = |AB| \cdot |AC| \cdot \sin\theta\)，三点共线时\(\theta=0\)或\(\pi\)，所以结果为0。

1
2
3
inline bool InLine(const Point &a, const Point &b, const Point &c) {
    return !dcmp((b - a).cross(c - a));
}

点到直线距离

点\(P\)到直线\(AB\)的距离，其实就是\(|\overrightarrow{AP}|\)在垂直于\(AB\)方向上的投影长度。

  • 公式：\(\text{距离} = |\overrightarrow{AP}| \cdot \sin\theta\)，其中\(\theta\)是\(AP\)与\(AB\)的夹角。

  • 叉积的几何意义：\(|\overrightarrow{AB} \times \overrightarrow{AP}| = |AB| \cdot |AP| \cdot \sin\theta\)，所以距离等于\(\frac{|\overrightarrow{AB} \times \overrightarrow{AP}|}{|AB|}\)。

1
2
3
double PointToLine(const Point &p, const Point &a, const Point &b) {
    return fabs((b - a).cross(p - a)) / (b - a).len();
}

点绕点逆时针旋转

点\(P\)绕\(O\)逆时针旋转\(\theta\)弧度，利用旋转矩阵：

  • \(x' = \cos\theta(x - x_0) - \sin\theta(y - y_0) + x_0\)
  • \(y' = \sin\theta(x - x_0) + \cos\theta(y - y_0) + y_0\)

旋转矩阵本质：

旋转矩阵是一种将点绕原点（或某个点）旋转一定角度后，得到新坐标的线性变换工具。它保证旋转后点到中心的距离不变，只改变与\(x\)轴的夹角。
（本节不展开推导，了解其作用即可。）

二维旋转矩阵的形式：

\[ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \]

也就是说，旋转后的新坐标 \([x', y']\)，等于"旋转矩阵"与原坐标 \([x, y]\) 的矩阵乘法结果。

直观理解：
- 旋转矩阵是一个 \(2 \times 2\) 的方阵。 - 只要用矩阵乘法，就能把任意点绕原点旋转任意角度。

1
2
3
4
5
Point Rotate(const Point &p, const Point &o, double theta) {
    double x = cos(theta) * (p.x - o.x) - sin(theta) * (p.y - o.y) + o.x;
    double y = sin(theta) * (p.x - o.x) + cos(theta) * (p.y - o.y) + o.y;
    return Point(x, y);
}

两直线平行

两直线\(AB\)与\(CD\)平行，当且仅当方向向量\(\overrightarrow{AB}\)与\(\overrightarrow{CD}\)平行。

  • 用叉积判断：\(\overrightarrow{AB} \times \overrightarrow{CD} = 0\)

  • 直观理解：\(|\overrightarrow{AB} \times \overrightarrow{CD}| = |AB| \cdot |CD| \cdot \sin\theta\)，平行时\(\theta=0\)或\(\pi\)，所以结果为0。

1
2
3
bool Parallel(const Point &a, const Point &b, const Point &c, const Point &d) {
    return !dcmp((b - a).cross(d - c));
}

两直线交点

设直线\(AB\)和\(CD\)不平行，求交点：

  • 利用参数方程和叉积，推导出交点公式

  • 原理解释：

\(t\) 表示 \(P\) 在 \(AB\) 上的位置比例，利用"面积比"来定位交点。

  • 公式推导：
    \[ t = \frac{(\vec{A} - \vec{C}) \times (\vec{D} - \vec{C})}{(\vec{B} - \vec{A}) \times (\vec{D} - \vec{C})} \]

    回想叉积公式，分子分母都对应的 底×高

    \[ P = \vec{A} + t(\vec{B} - \vec{A}) \]

  • 注意：分母为零时，说明两直线平行或重合。

  • 直观理解：交点是两条直线"方向量"线性组合的结果。

1
2
3
4
5
Point LineCross(const Point &a, const Point &b, const Point &c, const Point &d) {
    double u = (a - c).cross(d - c);
    double v = (b - a).cross(d - c);
    return a + (b - a) * (u / v);
}

线段相交

判断线段\(AB\)与\(CD\)是否相交：

  • 判断两端点分别在对方线段的两侧（叉积符号不同或为零）

  • 直观理解：如果\(C\)、\(D\)在\(AB\)两侧，\(A\)、\(B\)在\(CD\)两侧，则必有交点。

1
2
3
4
bool SegCross(const Point &a, const Point &b, const Point &c, const Point &d) {
    return dcmp((b - a).cross(c - a)) * dcmp((b - a).cross(d - a)) <= 0 &&
           dcmp((d - c).cross(a - c)) * dcmp((d - c).cross(b - c)) <= 0;
}

点到线段距离

点\(P\)到线段\(AB\)的距离：

  • 若投影在线段外，取到端点距离
  • 若投影在线段内，取到直线距离
1
2
3
4
5
double PointToSeg(const Point &p, const Point &a, const Point &b) {
    if(dcmp((b - a).dot(p - a)) < 0) return (p - a).len();
    if(dcmp((a - b).dot(p - b)) < 0) return (p - b).len();
    return fabs((b - a).cross(p - a)) / (b - a).len();
}

多边形与简单多边形

多边形：由有限个点按顺序连接而成的封闭图形。

凸多边形：任意两点连线都在多边形内部的多边形。

简单多边形：边与边只在顶点相交，不自交的多边形，可以是"凹"的。

凸多边形是简单多边形，简单多边形不一定是凸多边形

判断点在多边形内

射线法：从点向右发射水平射线，统计与多边形边界的交点数。

  • 交点数为奇数：点在多边形内
  • 交点数为偶数：点在多边形外

改进的射线法：处理边界情况，避免浮点误差。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool InPolygon(const Point &p, Point poly[], int n) {
    int flag = 0;
    for(int i = 0; i < n; i++) {
        Point p1 = poly[i];
        Point p2 = poly[(i + 1) % n];
        if(p.OnSeg(p1, p2)) return false; // 在边界上
        
        int k = dcmp(p1.cross(p2, p));
        int d1 = dcmp(p1.y - p.y);
        int d2 = dcmp(p2.y - p.y);
        if(k > 0 && d1 <= 0 && d2 > 0) flag++;
        if(k < 0 && d2 <= 0 && d1 > 0) flag--;
    }
    return flag != 0;
}

算法原理详解：

  1. 射线方向：从测试点P向右（x轴正方向）发射水平射线
  2. 叉积判断方向：p1.cross(p2, p) 判断点p相对于边p1→p2的位置
    • k > 0：p在边的左侧
    • k < 0：p在边的右侧
    • k = 0：p在边上
  3. y坐标比较：d1 = dcmp(p1.y - p.y), d2 = dcmp(p2.y - p.y)
    • d1 <= 0 && d2 > 0：边的起点在射线下方或同高，终点在射线上方
    • d2 <= 0 && d1 > 0：边的终点在射线下方或同高，起点在射线上方
  4. flag计数规则：
    • flag++：射线从下向上穿过边，且p在边的左侧
    • flag--：射线从下向上穿过边，且p在边的右侧
    • 最终 flag != 0 表示点在多边形内

为什么这样设计： - 避免了射线与顶点重合的边界情况 - 通过叉积方向判断，确保计数准确性 - 处理了凹多边形的复杂情况

多边形与圆的关系

点在圆内：点到圆心距离小于半径。

线段与圆相交：线段到圆心距离小于半径，且线段两端点不全在圆内。

多边形与圆相交：多边形有边与圆相交，或有顶点在圆内。

1
2
3
4
5
6
7
8
9
10
11
12
13
bool CircleIntersectPolygon(Point poly[], int n, Point center, double r) {
    for(int i = 0; i < n; i++) {
        Point a = poly[i], b = poly[(i + 1) % n];
        
        // 检查顶点是否在圆内
        if(center.Dis(a) <= r) return true;
        
        // 检查边是否与圆相交
        double dist = PointToSeg(center, a, b);
        if(dist <= r) return true;
    }
    return false;
}

简单多边形面积

有向面积：多边形面积有正负，逆时针为正，顺时针为负。

叉积法：利用叉积计算多边形面积，公式为：

\[ S = \frac{1}{2} \sum_{i=0}^{n-1} \vec{P_i} \times \vec{P_{i+1}} \]

其中 \(P_n = P_0\)（首尾相连）。

直观理解：将多边形分解为多个三角形，每个三角形的面积用叉积计算。

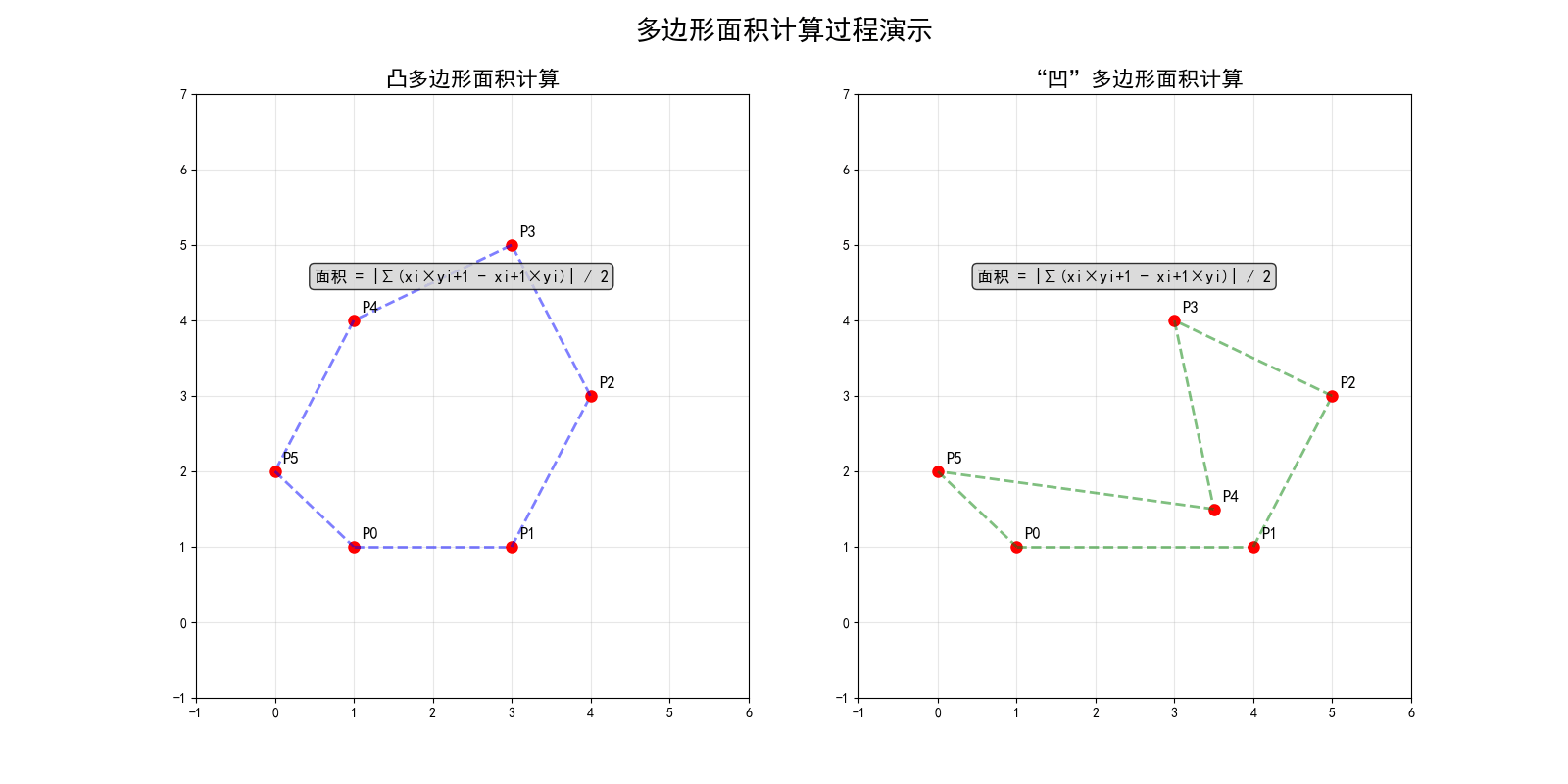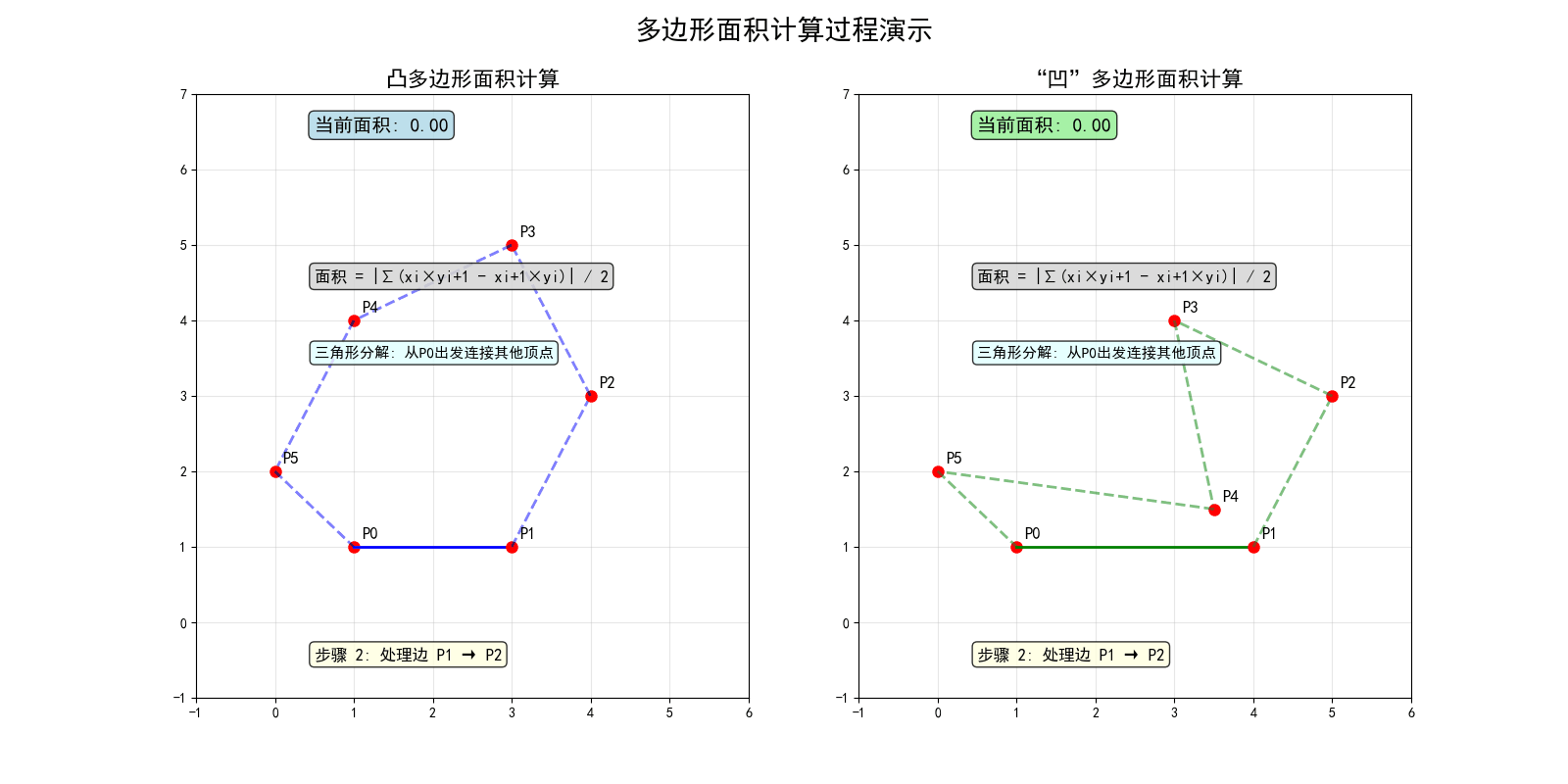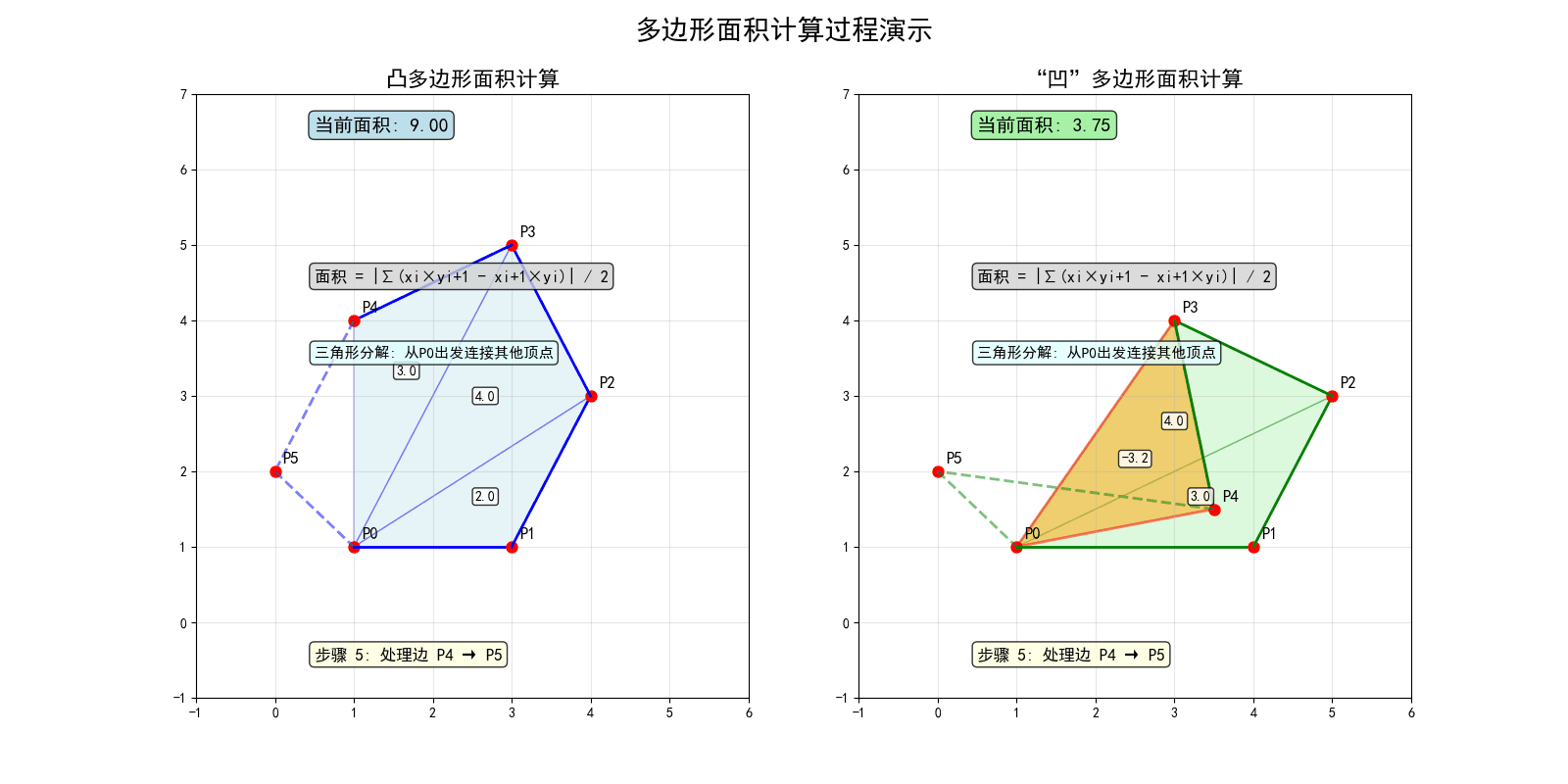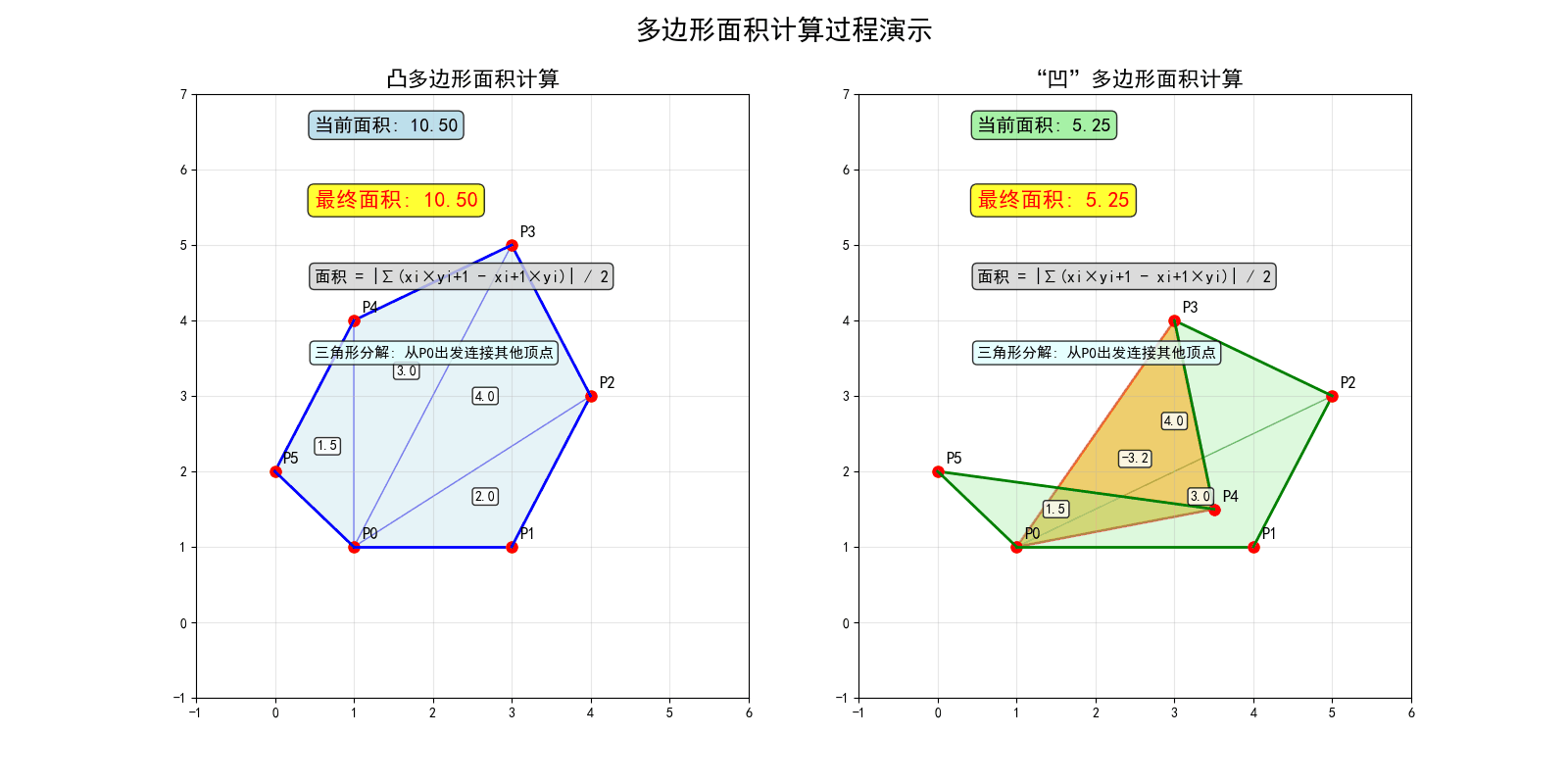
简单多边形面积的三角形分解过程中，某些三角形（如右图 P0-P3-P4）会出现"负面积"。这是因为这些三角形的顶点顺序为顺时针，面积公式自动赋予其负号。几何上，有"容斥"的味道：重叠部分被减去，最终得到正确的多边形面积。

多边形面积公式的优美之处就在于，无论凸多边形还是"凹"多边形，所有三角形的正负自动抵消，保证结果正确。

格林公式的离散形式：标准叉积公式 \(S = \frac{1}{2} \sum_{i=0}^{n-1} (x_i y_{i+1} - x_{i+1} y_i)\) 可以通过格林公式变形为更高效的形式。

变形过程： 1. 原始叉积：对于每条边 \(P_i \rightarrow P_{i+1}\)，计算 \(x_i \cdot y_{i+1} - x_{i+1} \cdot y_i\) 2. 重新组织：将每个顶点的贡献分离，对于顶点 \(P_i(x_i, y_i)\)，它参与的项有： - 作为起点：\(x_i \cdot y_{i+1}\)（贡献为正） - 作为终点：\(-x_{i+1} \cdot y_i\)（贡献为负） 3. 合并同类项：顶点 \(P_i\) 的总贡献 = \(x_i \cdot y_{i+1} - x_{i+1} \cdot y_i = y_i \cdot (x_{i-1} - x_{i+1})\)

优化效果：这样变形后，每个顶点只需要计算一次 \(y_i \cdot (x_{i-1} - x_{i+1})\)，避免了重复的模运算（如 (i+1) % n），提高了计算效率。

1
2
3
4
5
6
7
8
9
double PolygonArea(Point p[], int n) {
    if(n < 3) return 0.0;
    double s = p[0].y * (p[n - 1].x - p[1].x);
    p[n] = p[0];
    for(int i = 1; i < n; i++) {
        s += p[i].y * (p[i - 1].x - p[i + 1].x);
    }
    return fabs(s * 0.5); // 顺时针方向s为负
}

凸包（Convex Hull）

定义：包含所有点的最小凸多边形。

Graham扫描法：

  1. 找到最左下角的点作为起始点
  2. 按极角排序其他点（以起始点为原点，按逆时针方向排序）
  3. 用栈维护凸包，每次加入新点时检查是否破坏凸性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
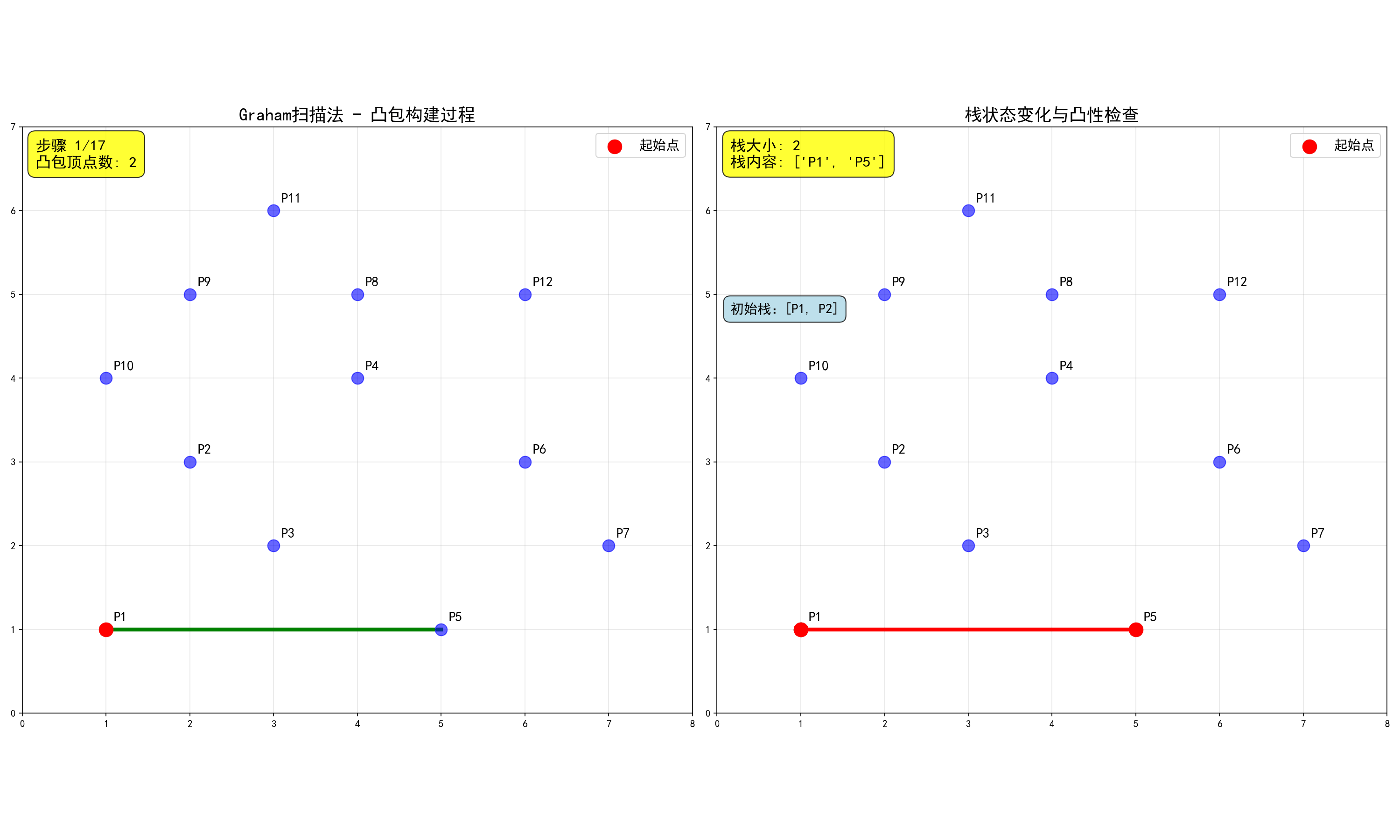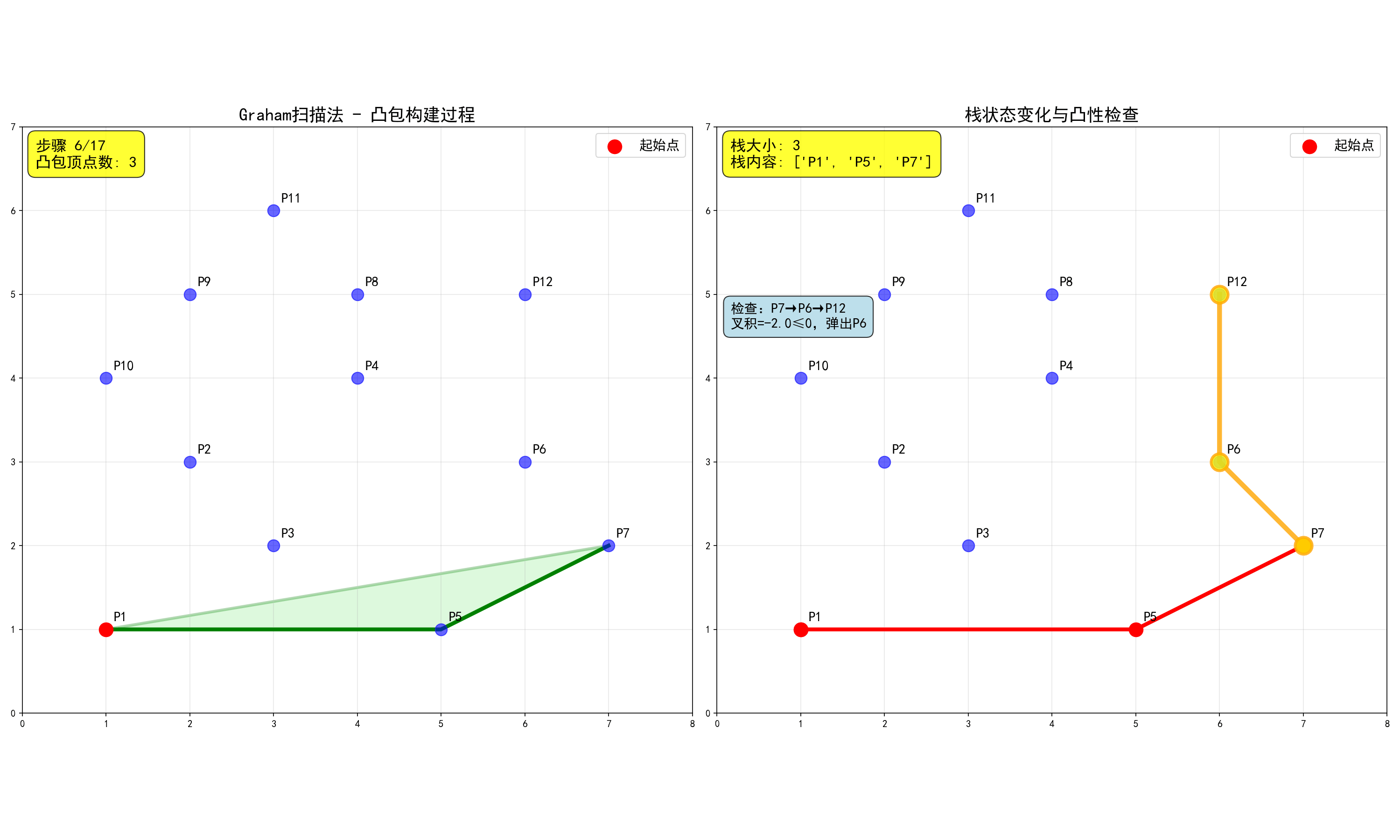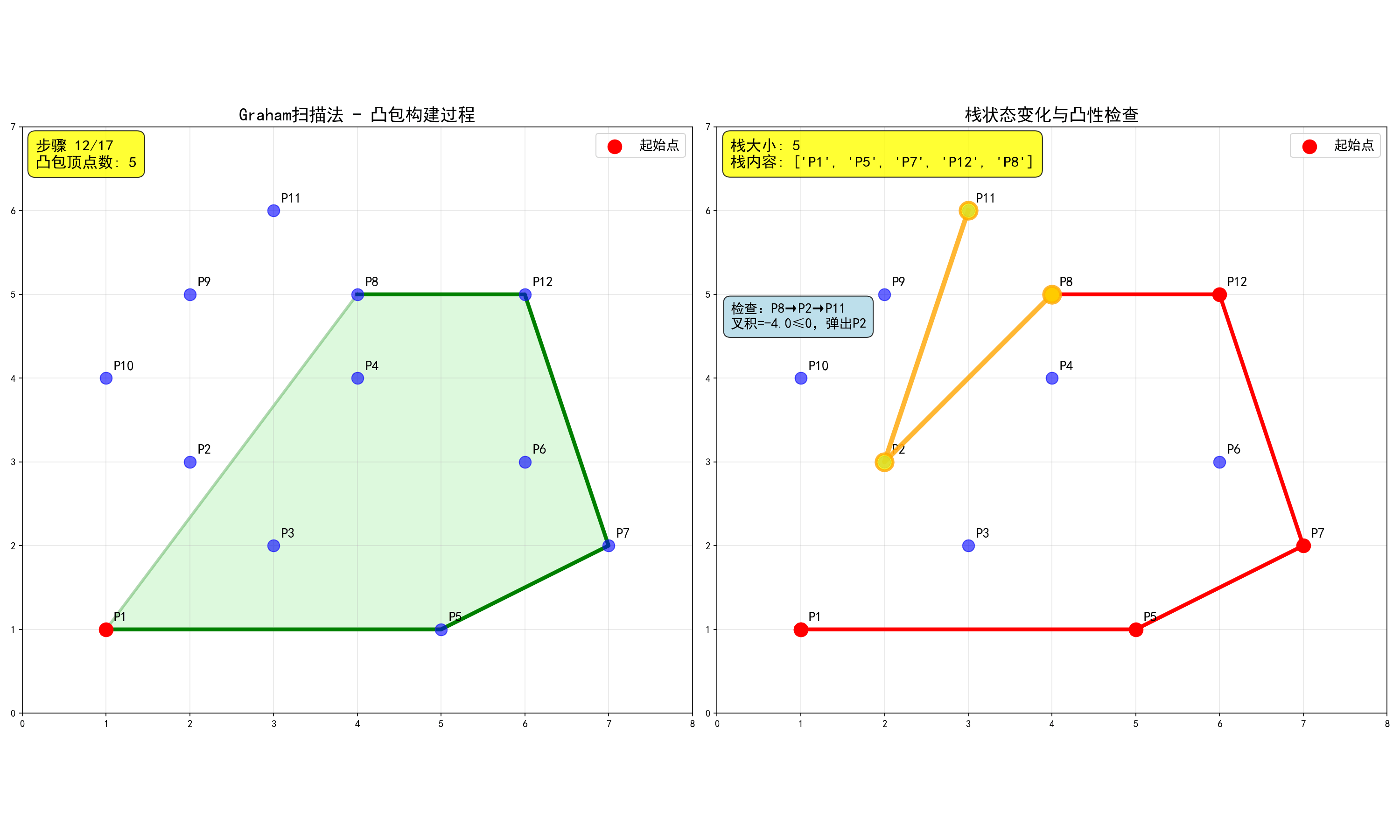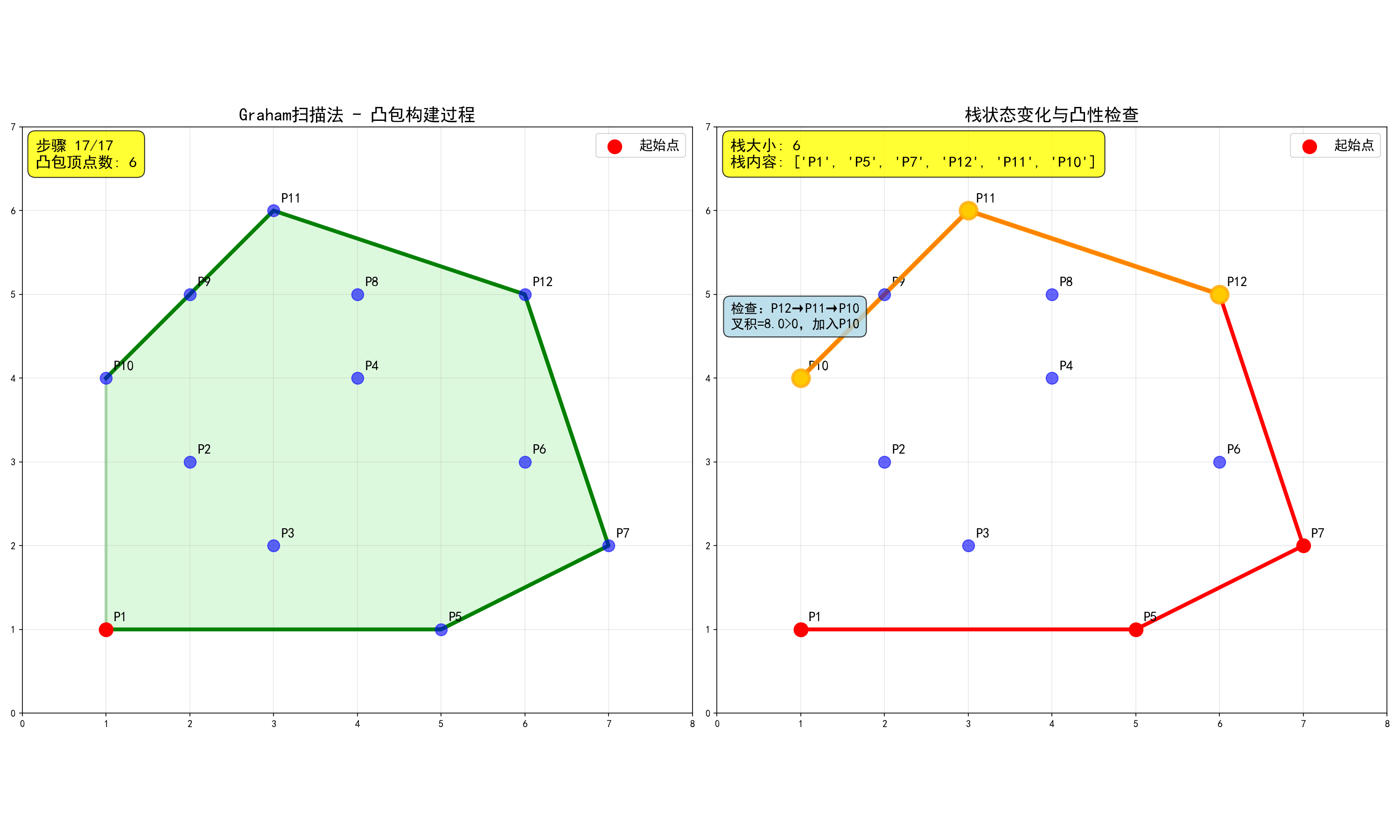
36
int Graham(Point p[], int n, Point res[]) {
    if(n < 3) {
        for(int i = 0; i < n; i++) res[i] = p[i];
        return n;
    }
    
    // 找到最左下角的点
    int k = 0;
    for(int i = 1; i < n; i++) {
        if(p[i].y < p[k].y || (p[i].y == p[k].y && p[i].x < p[k].x)) {
            k = i;
        }
    }
    swap(p[0], p[k]);
    
    // 按极角排序
    sort(p + 1, p + n, [&](const Point &a, const Point &b) {
        double cross = p[0].cross(a, b);
        if(dcmp(cross) != 0) return cross > 0;
        return p[0].Dis(a) < p[0].Dis(b);
    });
    
    // Graham扫描
    int top = 0;
    res[top++] = p[0];
    res[top++] = p[1];
    
    for(int i = 2; i < n; i++) {
        while(top > 1 && dcmp(res[top-2].cross(res[top-1], p[i])) <= 0) {
            top--;
        }
        res[top++] = p[i];
    }
    
    return top;
}

凸包的应用

  1. 最远点对：凸包上的点对可能是最远点对
  2. 最小包围圆：凸包的最小包围圆就是点集的最小包围圆
  3. 碰撞检测：两个凸多边形的碰撞检测比一般多边形简单

半平面交（Half Plane Intersection）

定义：多个半平面的交集，结果是一个凸多边形（可能为空）。

半平面：由一条直线分割平面得到的两个区域之一。

半平面表示

半平面由一条有向直线表示，即一个向量。向量的一侧为标记的半平面，通常约定为向量的左侧。

极角排序：对直线的方向向量进行极角排序。每条直线 \(s \rightarrow e\) 的方向向量 \(\vec{v} = (e_x - s_x, e_y - s_y)\) 与 \(x\) 轴正方向的夹角就是极角。极角小的排在前面，相同时距离原点近的排在前面。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
struct Line {
    Point s, e;  // 起点和终点，s->e向量表示有向直线
    double ang, d;  // 极角和距离参数
    
    Line() {}
    Line(Point s_, Point e_) {
        s = s_, e = e_;
        ang = atan2(e.y - s.y, e.x - s.x);  // 计算极角
        // 计算距离参数，用于排序
        if(dcmp(s.x - e.x)) 
            d = (s.x * e.y - e.x * s.y) / fabs(s.x - e.x);
        else 
            d = (s.x * e.y - e.x * s.y) / fabs(s.y - e.y);
    }
    
    // 判断两直线是否平行
    bool Parallel(const Line &l) {
        return !dcmp((e.x - s.x) * (l.e.y - l.s.y) - (e.y - s.y) * (l.e.x - l.s.x));
    }
    
    // 求两直线交点
    Point operator*(const Line &l) const {
        double u = s.cross(e, l.s), v = e.cross(s, l.e);
        return Point((l.s.x * v + l.e.x * u) / (u + v),
                    (l.s.y * v + l.e.y * u) / (u + v));
    }
    
    // 排序函数，优先极角，"左"边直线靠前
    bool operator<(const Line &l) const {
        return dcmp(ang - l.ang) ? ang < l.ang : d < l.d;
    }
};

算法步骤

  1. 排序：将所有半平面按极角排序
  2. 去重：去除极角相同的半平面
  3. 双端队列维护：用双端队列维护半平面交的边界
  4. 更新队列：每次加入新的半平面时，更新队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
bool HalfPlaneIntersection(Line l[], int n, Point cp[], int &m) {
    m = 0;
    sort(l, l + n);  // 按极角排序
    
    // 去重（相同极角的直线）
    int tn = 1;
    for(int i = 1; i < n; i++) {
        if(dcmp(l[i].ang - l[i-1].ang)) {
            l[tn++] = l[i];
        }
    }
    n = tn;
    
    if(n < 2) return false;
    
    // 双端队列
    int front = 0, rear = 1;
    Line deq[maxn];
    deq[0] = l[0];
    deq[1] = l[1];
    
    // 处理每条新的半平面
    for(int i = 2; i < n; i++) {
        // 检查队列尾部是否需要弹出
        while(front < rear && dcmp(l[i].s.cross(l[i].e, 
            deq[rear] * deq[rear-1])) < 0) {
            rear--;
        }
        // 检查队列头部是否需要弹出
        while(front < rear && dcmp(l[i].s.cross(l[i].e, 
            deq[front] * deq[front+1])) < 0) {
            front++;
        }
        deq[++rear] = l[i];
    }
    
    // 处理首尾相连的情况
    while(front < rear && dcmp(deq[front].s.cross(deq[front].e, 
        deq[rear] * deq[rear-1])) < 0) {
        rear--;
    }
    while(front < rear && dcmp(deq[rear].s.cross(deq[rear].e, 
        deq[front] * deq[front+1])) < 0) {
        front++;
    }
    
    if(rear <= front + 1) return false;  // 两条以下直线，没有围住
    
    // 保存结果（交点）
    for(int i = front; i < rear; i++) {
        cp[m++] = deq[i] * deq[i+1];
    }
    if(front < rear + 1) {
        cp[m++] = deq[front] * deq[rear];
    }
    
    // 去重和精度修复
    m = unique(cp, cp + m) - cp;
    for(int i = 0; i < m; i++) {
        cp[i].x = dcmp(cp[i].x) ? cp[i].x : 0;  // 负0误差修复
        cp[i].y = dcmp(cp[i].y) ? cp[i].y : 0;
    }
    
    return true;
}

多边形边平移求新核

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 将点沿a->b方向左侧垂直平移L
Point ParallelMove(Point a, Point b, Point ret, double L) {
    double len = a.Dis(b);
    return ret + Point((a.y - b.y) / len * L, (b.x - a.x) / len * L);
}

// 生成多边形的边向内平移L后的半平面集
void MakeNewPanels(Point p[], int n, Line l[], double L) {
    p[n] = p[0];
    for(int i = 0; i < n; i++) {
        l[i] = Line(ParallelMove(p[i], p[i+1], p[i], L),
                   ParallelMove(p[i], p[i+1], p[i+1], L));
    }
}

半平面交的应用

  1. 多边形求交：两个凸多边形的交集
  2. 碰撞检测：多个障碍物的安全区域
  3. 多边形收缩：将多边形边向内平移，求新的边界

模板参考

https://github.com/CSGrandeur/icpc_solution/blob/master/templates/ComputationalGeometry.md