35.数论入门

数论入门

入门数论，最大公约数、裴蜀定理、质数筛法、同余运算、欧拉函数、乘法逆元等。

最大公约数

最大公约数（Grand Central Dispatch, GCD）是能同时整除两个数的最大正整数。

给定正整数 \(a\) 和 \(b\) ，求两个数的最大公约数。

辗转相除法（欧几里得算法）

int GCD(int a, int b) {
    return b ? GCD(b, a % b) : a;
}

简要证明：

1. 基本概念：

• 设 \(g = \gcd(a,b)\) 表示 \(a\) 和 \(b\) 的最大公约数
• 因为 \(g\) 是 \(a\) 和 \(b\) 的公约数，所以 \(a\) 和 \(b\) 都可以被 \(g\) 整除
• 因此可以表示为：\(a = mg\)，\(b = ng\)，其中 \(m\) 和 \(n\) 是整数

2. 关键性质：\(m\) 和 \(n\) 一定互质（即 \(\gcd(m,n) = 1\)）

如果 \(m\) 和 \(n\) 不互质，那么 \(g\) 就不是最大公约数，这说明 \(g\) 已经包含了 \(a\) 和 \(b\) 的所有共同因子

3. 算法正确性：

• 当 \(b = 0\) 时，\(\gcd(a,0) = a\)，这是基本定义

• 当 \(b \neq 0\) 时，\(\gcd(a,b) = \gcd(b,a \bmod b)\)

  证明 \(\gcd(a,b) = \gcd(b,a \bmod b)\) ：

  • 设 \(d = \gcd(a,b)\)，则 \(d\) 能整除 \(a\) 和 \(b\)
  • 根据带余除法，\(a \bmod b = a - qb\)，其中 \(q\) 是 \(a \geq qb\) 的最大整数
  • 充分性：\(d\) 能整除 \(a\) 和 \(b\)，所以 \(d\) 也能整除 \(a - qb\)（即 \(a \bmod b\)）
  • 必要性：如果 \(d'\) 能整除 \(b\) 和 \(a \bmod b\)，那么 \(d'\) 也能整除 \(a = qb + (a \bmod b)\)
  • 因此，\(a\) 和 \(b\) 的公约数集合与 \(b\) 和 \(a \bmod b\) 的公约数集合完全相同
  • 所以它们的最大公约数也相同，即 \(\gcd(a,b) = \gcd(b,a \bmod b)\)

4. 算法终止：

每次递归调用时，第二个参数 \(b\) 都会变小。因为 \(a \bmod b < b\)，所以算法最终会到达 \(b = 0\) 的情况，因此算法一定会在有限步内终止。

复杂度分析

暴力枚举约数：

需要从1到\(\min(a,b)\)逐个尝试，时间复杂度：\(O(\min(a,b))\)

欧几里得算法：

每次递归调用时，\(b\) 至少减半，因此最多需要 \(\log \min(a,b)\) 次递归，时间复杂度：\(O(\log \min(a,b))\)

裵蜀定理（或称贝祖定理，Bézout's lemma）

对于任意两个不全为零的整数 \(a\) 和 \(b\)，存在整数（可以是负数） \(x\) 和 \(y\)，使得 \(ax + by = \gcd(a,b)\)。

证明

假设我们要证明：对于整数 \(a = 12\) 和 \(b = 8\)，存在整数 \(x\) 和 \(y\) 使得 \(12x + 8y = \gcd(12,8)\)。

1. 首先， \(\gcd(12,8) = 4\)
2. 使用辗转相除法：
   • \(12 = 8 \times 1 + 4\)
   • \(8 = 4 \times 2 + 0\)
3. 从第一个等式，我们可以得到：
   • \(4 = 12 - 8 \times 1\)
   • 这里 \(x = 1\), \(y = -1\) 就是我们要找的解

一般情况的证明思路：

1. 使用辗转相除法，可以得到一系列等式：
   • \(a = bq_1 + r_1\)
   • \(b = r_1q_2 + r_2\)
   • \(r_1 = r_2q_3 + r_3\)
   • ...
   • 直到 \(r_{n-1} = r_nq_{n+1} + 0\)
2. 最后一个非零余数 \(r_n\) 就是 \(\gcd(a,b)\)
3. 从最后一个非零等式开始，可以逐步回代，将 \(\gcd(a,b)\) 表示为 \(a\) 和 \(b\) 的线性组合

重要推论：

• 如果 \(a\) 和 \(b\) 互质（即 \(\gcd(a,b) = 1\)），那么存在整数 \(x\) 和 \(y\) 使得 \(ax + by = 1\)

• 反过来，如果存在整数 \(x\) 和 \(y\) 使得 \(ax + by = 1\)，那么 \(a\) 和 \(b\) 一定互质

  反证法：假设 \(a\) 和 \(b\) 不互质，即 \(\gcd(a,b) = d > 1\)

  • 那么 \(d\) 能整除 \(a\) 和 \(b\)，所以 \(d\) 也能整除 \(ax + by\)
  • 但 \(ax + by = 1\)，而 \(d > 1\) 不能整除 \(1\)，矛盾
  • 因此 \(a\) 和 \(b\) 必须互质

扩展：

推广到多个整数的情况：

• 对于 \(n\) 个不全为零的整数 \(a_1, a_2, \dots, a_n\)
• 存在整数 \(x_1, x_2, \dots, x_n\)，使得 \(a_1x_1 + a_2x_2 + \cdots + a_nx_n = \gcd(a_1, a_2, \dots, a_n)\)

例：线性和最小值

给定一个包含 \(n\) 个元素的整数序列 \(A\)，记作 \(A_1, A_2, A_3, \dots, A_n\)。

求另一个包含 \(n\) 个元素的待定整数序列 \(X\)，记 \(S = \sum_{i=1}^n A_i \times X_i\)，使得 \(S > 0\) 且 \(S\) 尽可能的小。

样例输入

2
4059 -1782

样例输出

99

分析：

1. 根据裵蜀定理的推广，\(S\) 一定是 \(\gcd(A_1, A_2, \dots, A_n)\) 的倍数，即 \(S = k \times \gcd(A_1, A_2, \dots, A_n)\)

   • 有同学举例 $8 - 3 = 5 $ 不是 \(8\) 和 \(3\) 的公约数，这与论述不矛盾， \(S\) 一定是 公约数的倍数， \(5\) 是 \(1\) 的倍数。

2. 要使 \(S > 0\) 且最小，\(k\) 必须取最小的正整数，即 \(k = 1\)，因此 \(S = \gcd(A_1, A_2, \dots, A_n)\)
3. 对于 \(A_{i}\) 是负数的情况：因为 \(\gcd(a,b) = \gcd(|a|,|b|)\)，例如：\(\gcd(12,-8) = \gcd(12,8) = 4\)，所以可以直接对序列中的每个数取绝对值，再求最大公约数。

简单的一串GCD搞定：

#include<cstdio>
#include<cmath>

int GCD(int a, int b) {
    return b ? GCD(b, a % b) : a;
}

int main() {
    int n, a = -1, b;
    scanf("%d", &n);
    while(n --) {
        scanf("%d", &b);
        a = a == -1 ? b : GCD(a, abs(b));
    }
    printf("%d\n", a);
    return 0;
}

质数与质数筛

质数（素数）是指大于1的自然数中，除了1和它本身外不再有其他因数的数。

判断一个数 \(n\) 是否为质数，只需要检查 \(2\) 到 \(\sqrt{n}\) 之间的所有整数是否能整除 \(n\)。如果都不能整除，则 \(n\) 是质数。

bool isPrime(int n) {
    if (n <= 1) return false;  // 1和负数不是质数
    if (n == 2) return true;   // 2是质数
    if (n % 2 == 0) return false;  // 偶数不是质数（除了2）
    
    // 只需要检查到sqrt(n)
    for (int i = 3; i * i <= n; i += 2) {
        if (n % i == 0) return false;
    }
    return true;
}

时间复杂度：\(O(\sqrt{n})\)

当需要枚举质数，或者有大量数字要快速判断是否是质数时，一个一个\(O(\sqrt(n))\) 地判断就力不从心了。

可以通过筛选的方法一次性预处理得到不超过 \(n\) 的所有质数。

埃拉托斯特尼筛法（sieve of Eratosthenes）

简称埃氏筛法，筛掉所有有非 \(1\) 约数的数（合数），剩下的就是质数了。

合数都是由一系列质因数构成的，那么从小到大考虑每个正整数 \(x\) ，把比它大的倍数 \(y\) 都标为合数，最后没标记的就是质数了。

进一步，因为从小到大考虑的时候，在之前的数考虑过程中，每个待考虑的数 \(x\) 已经能确定它是否是质数了，那么要考虑的 \(x\) 就可以跳过所有合数，更加快捷。

复杂度\(O(nloglogn)\)，证明略，可搜索网上资料。

bool isPrime[maxn];
void SetPrime() {
    memset(isPrime, 1, sizeof(isPrime));
    isPrime[0] = isPrime[1] = false;
    for(int i = 2; i * i < maxn; i ++) {
        if(!isPrime[i]) {
            continue;
        }
        for(int j = i * i; j < maxn; j += i) {
            isPrime[j] = false;
        }
    }
}

欧拉线性筛法

如果能让每个合数都只被标记一次，那么时间复杂度就可以降到 \(O(n)\) 了。

核心思想：让每个合数只被它的最小质因子筛掉。

具体实现的关键点：

1. 使用数组 prime 记录已经找到的质数
2. 对于每个数 \(i\)：
   • 如果 \(i\) 是质数，加入质数表
   • 用 \(i\) 和质数表中的质数相乘，标记合数
   • 当 \(i\) 能被当前质数整除时，停止标记

为什么这样能保证每个合数只被标记一次？

设合数 \(n\) 的最小质因子为 \(p\)

• 当 \(i = \frac{n}{p}\) 时，\(n\) 会被标记
• 因为 \(p\) 是 \(n\) 的最小质因子，所以 \(\frac{n}{p}\) 的所有质因子都大于等于 \(p\)
  • 当 \(i < \frac{n}{p}\) 时：
    • 要么\(i\)包含质因数\(p\)，那么会if(i % prime[j] == 0) break;
    • 要么\(i\)要乘以比\(p\)大的质因数才能接近\(n\)，但这样它们都不包含\(p\)必然无法得到\(n\)
  • 当 \(i > \frac{n}{p}\) 时，\(i\) 乘以任何质数都会大于 \(n\)

因此，每个合数 \(n\) 只会在 \(i = \frac{n}{p}\) 时被标记一次，其中 \(p\) 是 \(n\) 的最小质因子。

bool isPrime[maxn];
int prime[maxm], ptp;
void SetPrime() {
    ptp = 0;
    memset(isPrime, 1, sizeof(isPrime));
    isPrime[0] = isPrime[1] = false;
    for(int i = 2; i < maxn; i ++) {
        if(isPrime[i]) prime[ptp ++] = i;
        for(int j = 0; j < ptp && i * prime[j] < maxn; j ++) {
            isPrime[i * prime[j]] = false;
            if(i % prime[j] == 0) break;
        }
    }
}

同余的基本概念

如果两个整数 \(a\) 和 \(b\) 除以正整数 \(m\) 的余数相同，我们就说 \(a\) 和 \(b\) 对模 \(m\) 同余，记作： \(a \equiv b \pmod{m}\)

例如：

• \(7 \equiv 2 \pmod{5}\)，因为 \(7\) 和 \(2\) 除以 \(5\) 的余数都是 \(2\)
• \(12 \equiv 0 \pmod{3}\)，因为 \(12\) 和 \(0\) 除以 \(3\) 的余数都是 \(0\)

同余的基本性质：

1. 如果 \(a \equiv b \pmod{m}\)，那么 \(a - b\) 能被 \(m\) 整除
2. 如果 \(a \equiv b \pmod{m}\)，那么 \(a + c \equiv b + c \pmod{m}\)
3. 如果 \(a \equiv b \pmod{m}\)，那么 \(ac \equiv bc \pmod{m}\)

基于基本性质可知：

• 在加减乘运算过程中，可以随时对中间结果取模，最终结果不变
• 例如：计算 \((a + b) \times c \bmod m\) 时，可以：
  1. 先计算 \(a + b \bmod m\)
  2. 再乘以 \(c\) 后取模
  3. 结果与直接计算 \((a + b) \times c \bmod m\) 相同

这个性质在计算大数时特别有用，可以避免中间结果溢出。

注意这里"任意中间结果取模"是在加减乘运算过程中，不包含除法，除法运算的取模要考虑另外一个知识点——乘法逆元，将在后续内容中学习。

这就是为什么一些数据很大的题，要求结果对 \(10^{9}+7\)、 \(998244353\) 等这种很大的数取模时，可以在中间任意步骤取模以防溢出 int 或 long long。

扩展了解：线性同余方程、中国剩余定理

欧拉函数

欧拉函数 \(\varphi(n)\) 表示小于等于 \(n\) 且与 \(n\) 互质的数的个数。例如：

• \(\varphi(1) = 1\)（1与自身互质）
• \(\varphi(6) = 2\)（1和5与6互质）
• 当 \(n\) 是质数时，\(\varphi(n) = n - 1\)（因为质数与所有小于它的数都互质）

欧拉函数的计算公式：\(\varphi(n) = n \prod_{p|n} (1-\frac{1}{p})\)，其中 \(p\) 是 \(n\) 的所有质因数。

1. 一个数与 \(n\) 不互质，当且仅当它能被 \(n\) 的某个质因数整除
2. 对于 \(n\) 的每个质因数 \(p\)：在 \(1\) 到 \(n\) 中，有 \(\frac{n}{p}\) 个数能被 \(p\) 整除，所以有 \(n(1-\frac{1}{p})\) 个数不能被 \(p\) 整除
3. 对于不同的质因数，它们的影响是独立的：一个数能被某个质因数整除，与它是否能被其他质因数整除无关
4. 因此，最终与 \(n\) 互质的数的个数就是 \(n\) 连续乘以每个质因数 \(p\) 的 \((1-\frac{1}{p})\)

例如，对于 \(n = 12\)：

• 质因数为 \(2\) 和 \(3\)
• \(\varphi(12) = 12 \times (1-\frac{1}{2}) \times (1-\frac{1}{3}) = 12 \times \frac{1}{2} \times \frac{2}{3} = 4\)
• 确实，\(1, 5, 7, 11\) 这四个数与 \(12\) 互质

直接计算欧拉函数

1. 从2开始尝试每个可能的质因数
2. 找到一个质因数 \(i\) 后，将 \(n\) 除以 \(i\) 的幂，同时更新结果
3. 最后如果 \(tn > 1\)，说明 \(tn\) 是一个大于 \(\sqrt{n}\) 的质因数

int Euler(int n) {
    int res = n, tn = n;
    for(int i = 2; i * i <= tn; i ++) {
        if(tn % i) continue;
        res = res / i * (i - 1);
        while(tn % i == 0) tn /= i;
    }
    if(tn > 1) res = res / tn * (tn - 1);
    return res;
}

代码中的关键步骤解释：

while(tn % i == 0) tn /= i;

这行代码用于去除 \(n\) 中质因数 \(i\) 的所有幂，对于 \(n = 12 = 2 \times 2 \times 3\)，当 \(i = 2\) 时，循环会执行两次，将 \(tn\) 从 \(12\) 变成 \(3\)，这样确保每个质因数只被处理一次。

if(tn > 1) res = res / tn * (tn - 1);

这个判断处理的是大于 \(\sqrt{n}\) 的质因数，这样的质因数至多只会有 1 个。例如：对于 \(n = 35 = 5 \times 7\)，当 \(i = 5\) 时，\(tn\) 会变成 \(7\)，因为 \(7 > \sqrt{35}\)，要在循环后单独处理。

欧拉函数打表

需要随机使用很多不同的数的欧拉函数值时，预处理打好表。

1. 初始化每个数的待计算欧拉函数值为自身
2. 从小到大遍历每个数，如果这个数等于它的欧拉函数值，说明它是质数
3. 对于每个质数，更新它的所有倍数的欧拉函数值

这样每个数都会被它的所有质因数处理一次，最终得到正确的欧拉函数值

std::vector<int> el; // 累加求和的话注意 long long
void EulerList(int maxn) {
    el.resize(maxn + 10);
    for(int i = 1; i <= maxn; i ++) {
        el[i] = i;
    }
    for(int i = 2; i <= maxn; i ++) {
        if(el[i] != i) continue;
        for(int j = i; j <= maxn; j += i) {
            el[j] = el[j] / i * (i - 1);    // n * (1 - 1/p)
        }
    }
}

例：求互质个数

计算在 \([1, 2023^{2023}]\) 范围内与 \(2023\) 互质的数的个数。

分析：

欧拉函数 \(\varphi(n)\) 是 \(n\) 以内与 \(n\) 互质的数的个数，但题目区间是 \([1, n^{n}]\)。

注意到 如果一个数与 \(n\) 互质，则必然与 \(n^{n}\) 互质，那么这道题等于求 \(\varphi(n^n)\)，根据欧拉函数的计算方式，从 \(n^n\) 摘出一个 \(n\)计算 \(\varphi(n)\) ，再乘上 \(n^{n-1}\) 与 \(\varphi(n^n)\) 也是相等的，结合快速幂取模可解。

这道题给的数字 2023 质因数分解比较简单，计算欧拉函数时不涉及因为有除法而无法完成同余计算的问题，故可以直接计算。

#include<cstdio>
#include<cmath>
const int mod = 1e9 + 7;

int PowMod(int a, int n) {
    int ret = 1;
    for(; n; n >>= 1, a = 1LL * a * a % mod)
        if(n & 1) ret = 1LL * ret * a % mod;
    return ret;
}
int Euler(int n) {
    int res = n, tn = n;
    for(int i = 2; i * i <= tn; i ++) {
        if(tn % i) continue;
        res = 1LL * res * (i - 1) / i % mod;
        while(tn % i == 0) tn /= i;
    }
    if(tn > 1) res = res / tn * (tn - 1);
    return res;
}

int main() {
    int n;
    scanf("%d", &n);
    printf("%lld\n", 1LL * Euler(n) * PowMod(n, n - 1) % mod);
    return 0;
}

乘法逆元

数学上的乘法逆元就是指直观的倒数，即 \(a\) 的逆元是 \(\frac{1}{a}\)，也即与 \(a\) 相乘得 \(1\) 的数。\(a \cdot x = 1\)，则 \(x\) 是 \(a\) 的乘法逆元。

而在对特定数取模时，也有一个乘法逆元概念，如果 \(a \cdot x \bmod b = 1\)，则 \(x\) 是 \(a\) 的关于 \(mod b\) 的乘法逆元。

设 \(m\) 是一个很大的数，\(a\)、\(b\) 已知，预期要计算（假设答案为 \(c\)）：

\[ \frac{m}{a} \bmod b \]

对于 \(a\) 的逆元 \(d\)，能够满足

\[ m \cdot d \bmod b = \frac{m}{a} \bmod b = c \]

在有些问题中，无法计算最终值很大的 \(m\)，只能得到基于同余的一个中间值 \(m \bmod b = e\) 来计算 \(\frac{e}{a} \bmod b\)，而 \(e\) 可能无法整除 \(a\)：

比如计算 \(\frac{18}{3} \bmod 7 = 6\)，但如果先根据同余计算了 \(18 \bmod 7 = 4\)，后续 \(\frac{4}{3}\) 就无法整除了。

用 \(a\) 的逆元 \(d\)，来计算 \(e \cdot d \bmod b\)。

除数 \(3\) 关于模数 \(7\) 的逆元 \(5\)（根据逆元定义，\(5\) 符合 \(3 \cdot 5 \bmod 7 = 1\)），从而，用乘以 \(5\) 代替除以 \(3\)。

上述第二步除法变乘法：\(4 / 3 \rightarrow 4 \cdot 5 = 20\)，\(20 \bmod 7 = 6\)，从而也计算出了正确的结果 \(6\)。

求逆元的三种方法

更详细资料见：乘法逆元

1. 扩展欧几里得算法

   • 适用范围：模数 \(m\) 不要求是质数，只要 \(a\) 和 \(m\) 互质即可
   • 时间复杂度：\(O(\log m)\)
   • 最常用、最安全的求逆元方式

typedef long long LL;
LL ExGCD(LL a, LL b, LL &x, LL &y) {
    // x, y 为引用传参，故最终程序结束后，x,y会被赋值为可行解
    if(b == 0) {
        // 递归终点，ax+by=GCD(a,b)的b为0，故方程变为
        // ax=a，则可行解可以是 x=1, y=0
        x = 1, y = 0;
        return a;
    }
    LL d = ExGCD(b, a % b, x, y), t = x;
    x = y, y = t - a / b * x;
    return d;  // 这里返回值是GCD(a,b)的结果，即最大公约数
}
int ExGcdInv(int a, int b) {
    int x, y;
    ExGCD(a, b, x, y);
    return x;
}

1. 费马小定理
   • 适用范围：模数 \(m\) 必须是质数
   • 时间复杂度：\(O(\log m)\)
   • 原理：若 \(m\) 为质数，则 \(a^{m-1} \equiv 1 \pmod{m}\)，因此 \(a^{-1} \equiv a^{m-2} \pmod{m}\)

int PowMod(int a, int n, int mod) {
    int ret = 1;
    while(n) {
        if(n & 1) ret = ret * a % mod;
        a = a * a % mod;
        n >>= 1;
    }
    return ret;
}
int FermatInv(int a, int b) {
    return PowMod(a, b - 2, b);
}

2. 递推求逆元
   • 适用范围：模数 \(m\) 必须是质数
   • 时间复杂度：\(O(\log m)\)
   • 递推公式：\(inv(a) \equiv -\lfloor m/a \rfloor \cdot inv(m \bmod a) \pmod{m}\)

LL Inv(LL a, LL b) {
    if(a == 1) return 1;
    return (b - b / a) * Inv(b % a, b) % b;
}

逆元打表

当需要频繁使用不同数的逆元时，可以预处理打表：

int inv[maxn];
void GetInv(int mod) {
    inv[1] = 1;
    for(int i = 2; i < mod; i ++)
        inv[i] = 1LL * (mod - mod / i) * inv[mod % i] % mod;
}

数论分块

例：除法向下取整求和

向下取整（floor 运算）：

\[ \left\lfloor \frac{n}{i} \right\rfloor \]

例如： \[ \left\lfloor \frac{5}{2} \right\rfloor = 2, \quad \left\lfloor \frac{10}{3} \right\rfloor = 3 \]

C 语言中的 \(int\) 运算默认向下取整。

给定 \(n\)（\(10^{12}\) 级别），求 \(i\) 从 \(1\) 到 \(n\) 的所有 \(\left\lfloor \frac{n}{i} \right\rfloor\) 的和，即： \[ \sum_{i=1}^{n} \left\lfloor \frac{n}{i} \right\rfloor \]

以 \(n=11\) 为例，

观察 \(x=4\sim5\)、\(x=6\sim11\) 的分段情况。

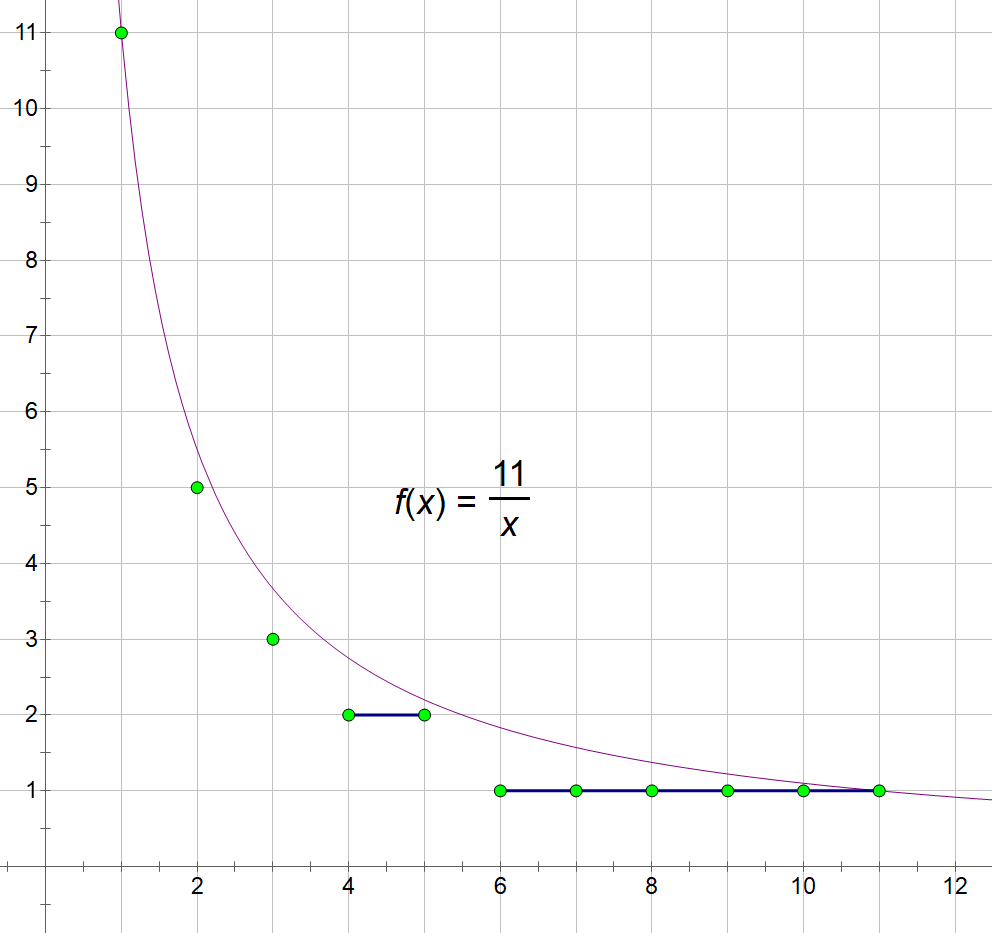
引理：\(n/d\) 向下取整的不同值个数不超过 \(2\) 倍的 \(n\) 的平方根

\[ \forall n \in \mathbb{N}_+,\ \left| \left\{ \left\lfloor \frac{n}{d} \right\rfloor \mid d \in \mathbb{N}_+,\ d \leq n \right\} \right| \leq \left\lfloor 2\sqrt{n} \right\rfloor \]

证明：

• \(d \leq \left\lfloor \sqrt{n} \right\rfloor\) 时，\(\left\lfloor \frac{n}{d} \right\rfloor\) 有 \(\sqrt{n}\) 种取值。
• \(d > \left\lfloor \sqrt{n} \right\rfloor\) 时，\(\left\lfloor \frac{n}{d} \right\rfloor \leq \left\lfloor \sqrt{n} \right\rfloor\)，故也至多 \(\left\lfloor \sqrt{n} \right\rfloor\) 种取值。

因此总的不同取值个数不超过 \(2\sqrt{n}\)。

如何高效枚举 \(\left\lfloor \frac{n}{i} \right\rfloor\) 的所有不同值？

对于每个 \(i\)，找到 \(\left\lfloor \frac{n}{i} \right\rfloor\) 的"右端点"，即最大的 \(j\)，使得 \(\left\lfloor \frac{n}{i} \right\rfloor = \left\lfloor \frac{n}{j} \right\rfloor\)。

• \(i=4\) 时，\(j=5\)
• \(i=6\) 时，\(j=11\)

\(\left\lfloor \frac{n}{i} \right\rfloor = \left\lfloor \frac{n}{j} \right\rfloor\) 的最大 \(j\) 是：

\[ j = \left\lfloor \frac{n}{\left\lfloor \frac{n}{i} \right\rfloor} \right\rfloor \]

简要证明：

令 \(k = \left\lfloor \frac{n}{i} \right\rfloor\)，变量 \(t\) 满足 \(\left\lfloor \frac{n}{t} \right\rfloor = \left\lfloor \frac{n}{i} \right\rfloor\)，\(j\) 为最大的 \(t\)。

• \(k \leq \frac{n}{t}\)
• \(\left\lfloor \frac{n}{k} \right\rfloor \geq \left\lfloor \frac{n}{n/t} \right\rfloor = \left\lfloor t \right\rfloor = t\)
• \(t\) 可取的最大值为 \(\left\lfloor \frac{n}{k} \right\rfloor\)
• \(j = \max(t) = \left\lfloor \frac{n}{k} \right\rfloor = \left\lfloor \frac{n}{\left\lfloor \frac{n}{i} \right\rfloor} \right\rfloor\)

高效计算 \(\sum\limits_{i=1}^n \left\lfloor \frac{n}{i} \right\rfloor\)

int ret = 0;
for(int i = 1, j; i <= n; i = j + 1) {
    j = n / (n / i);
    ret += (n / i) * (j - i + 1);
}

例：两个除法向下取整

\[ \sum_{i=1}^n \left\lfloor \frac{n}{i} \right\rfloor \left\lfloor \frac{m}{i} \right\rfloor \]

相对上一个问题，两个除法只是把相等的块分的更细了而已，用更小步去迭代即可。

int ret = 0;
for(int i = 1, j; i <= n; i = j + 1) {
    j = std::min(n / (n / i), m / (m / i));
    ret += (n / i) * (m / i) * (j - i + 1);
}

例：乘个别的

\[ \sum_{i=1}^ni\lfloor\frac{n}{i}\rfloor \]

观察发现，每段稳定的 \(k\) 对应一段有规律变化值，仍然可以按稳定值分块后，对每一块的规律变化值另外计算。

int ret = 0;
for(int i = 1, j; i <= n; i = j + 1) {
    j = n / (n / i);
    ret += (n / i) * (i + j) * (j - i + 1) / 2;
}

例：通用化

\[ \sum_{i=1}^{\min{n_t}} f(i)\prod_{各式各样的g_t,n_t} g_{t}(\lfloor \frac{n_t}{i} \rfloor) \]

例如

\[ \sum_{i=1}^{\min(n_t)} fib_{i}\prod_{t=1}^m \lfloor \frac{n_t}{i} \rfloor \]

其中 \(fib\) 表示斐波那契数列

提示：预处理 \(f(i)\) 的前缀和，在 \(\frac{n_{t}}{i}\) 的分段节点中每次选最小节点

自行尝试

例：一些变通

计算 \(\sum_{i=1}^{n}(k \mod i)\)

提示：\(k \mod i == k - i*\lfloor \frac{k}{i} \rfloor\)

剩下的自行尝试

注意事项

• 注意是否需要 long long
• 别只盯着结果，看看中间步骤是否超 int
• 检查求和范围，“右端点”计算、for循环范围也会有陷阱