34.字符串算法

字符串算法

KMP、AC自动机、字符串哈希、最小表示法。

KMP

mStr = "aaaaabbcaaab"
tStr = "aaab"

如何找到 tStr 在 mStr 中出现的位置？如何找出出现的次数？复杂度是多少？

int Index1(char mStr[], char tStr[]) {
  int i, j;
  // 遍历主字符串的每个位置作为可能的起始位置
  for(i = 0; mStr[i]; i ++) {
    // 从当前位置i开始，逐个字符比较mStr和tStr
    // 当tStr[j]为'\0'（字符串结束）或字符不匹配时退出循环
    for(j = 0; tStr[j] && mStr[i + j] == tStr[j]; j ++);    // 这里有分号
    
    // 如果tStr[j]为'\0'，说明tStr已经完全匹配
    if(!tStr[j]) {
        return i;  // 返回匹配的起始位置
    }
  }
  return -1;  // 未找到匹配，返回-1
}

暴力匹配算法的时间复杂度为 \(O(m \times n)\)，其中 \(m\) 是主串长度，\(n\) 是模式串长度。要改进这个算法，需要思考两个方向：

1. 比较操作的优化
   • 字符串比较必须逐个字符进行，这是无法避免的
   • 因此，优化的重点不在于减少单次比较的复杂度
2. 比较次数的优化
   • 暴力匹配中，每次失配后都从主串的下一个位置重新开始比较
   • 这导致了很多不必要的比较操作
   • 例如：当模式串为"aaab"时，如果前三个'a'都匹配，最后一个'b'失配，下一次比较时，我们其实已经知道前两个'a'是匹配的

利用已知信息

在暴力匹配中，每次失配后我们都从主串的下一个位置重新开始比较，这导致了很多重复的比较操作。例如，当模式串为"aaab"时，如果前3个'a'都匹配，最后一个'b'失配，右挪 1 位进行下一次比较时，我们其实已经知道有 2 个'a'是匹配的。

关键问题在于：如何利用已经比较过的信息？当发生失配时，我们是否可以从之前的匹配结果中获取有用信息？能否避免重复比较已经确定匹配的部分？

这些思考最终引出了KMP算法的核心思想：通过预处理模式串，构建 \(next\) 数组，在失配时利用已知信息快速移动模式串，从而减少比较次数。KMP算法的精髓就在于，它能够从失败的匹配中学习，利用已经匹配的信息来指导下一次匹配的位置。

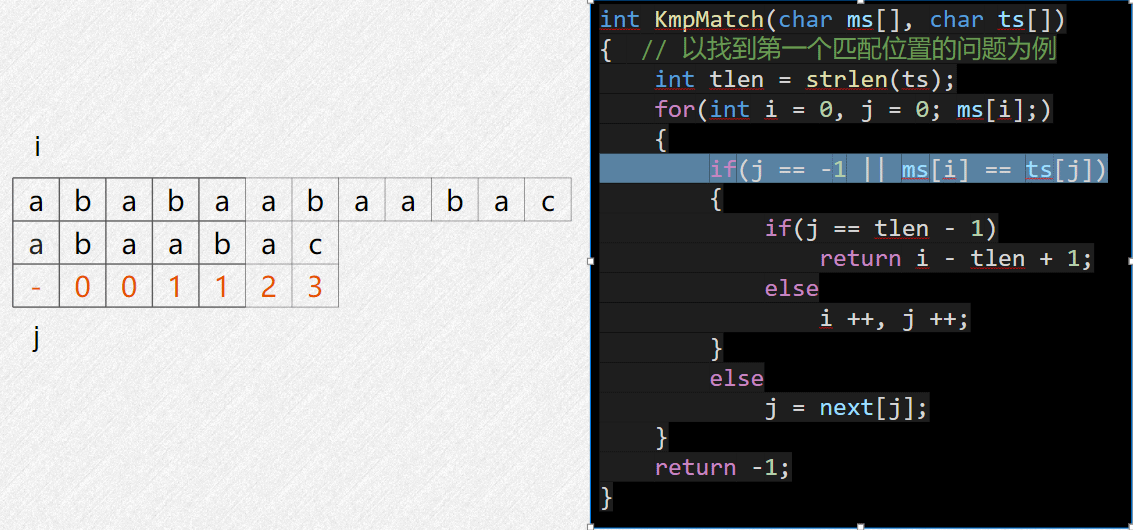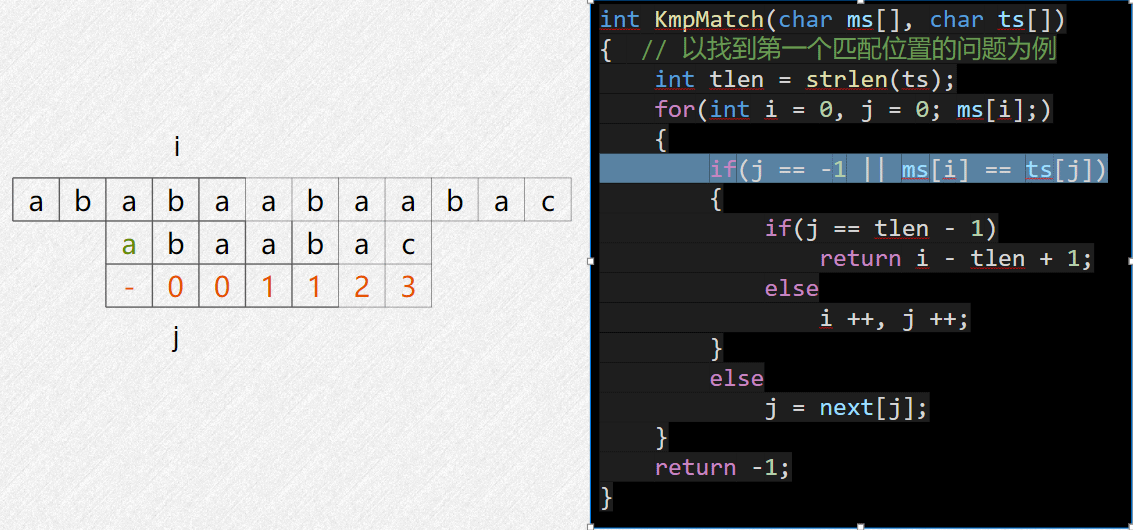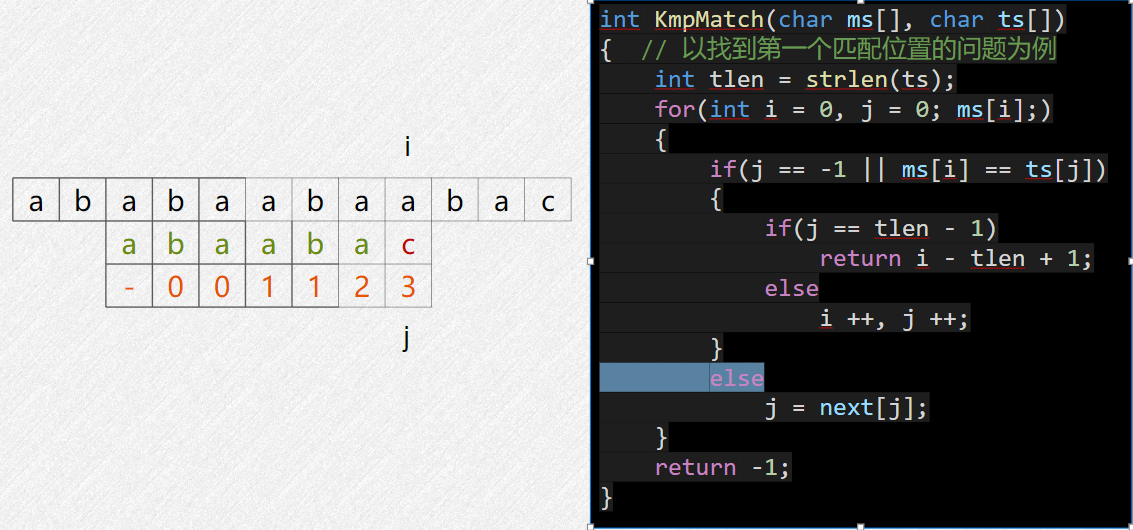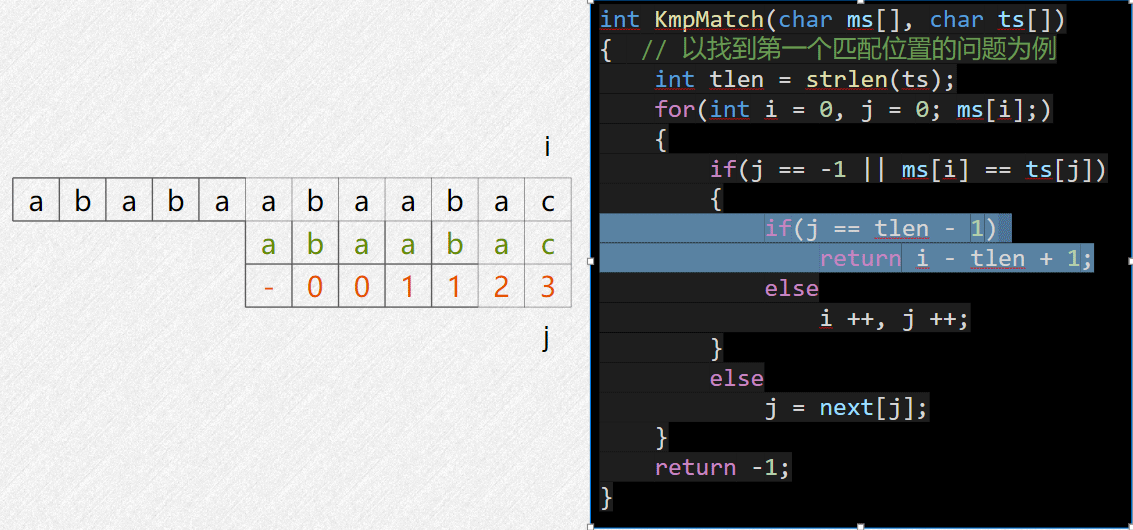
核心思想：找到已经匹配的前缀串的最长相等前后缀，把它挪到这个后缀开头的位置进行匹配

如上图，成功匹配的前缀串是 abcab，它的最长相等前后缀是 ab，那么下一次比较就直接让它开头的 ab 对齐到后面的 ab 位置去比对。

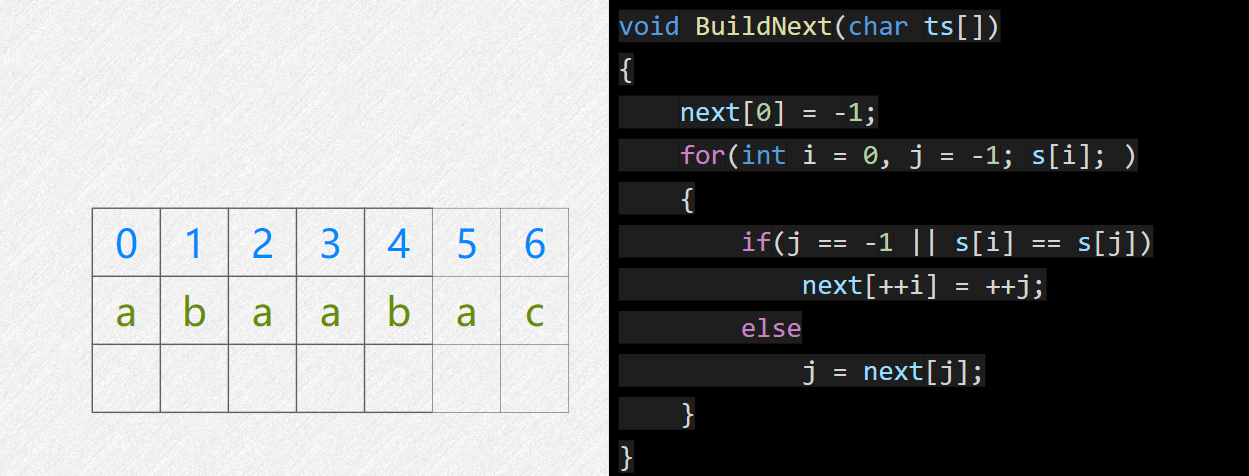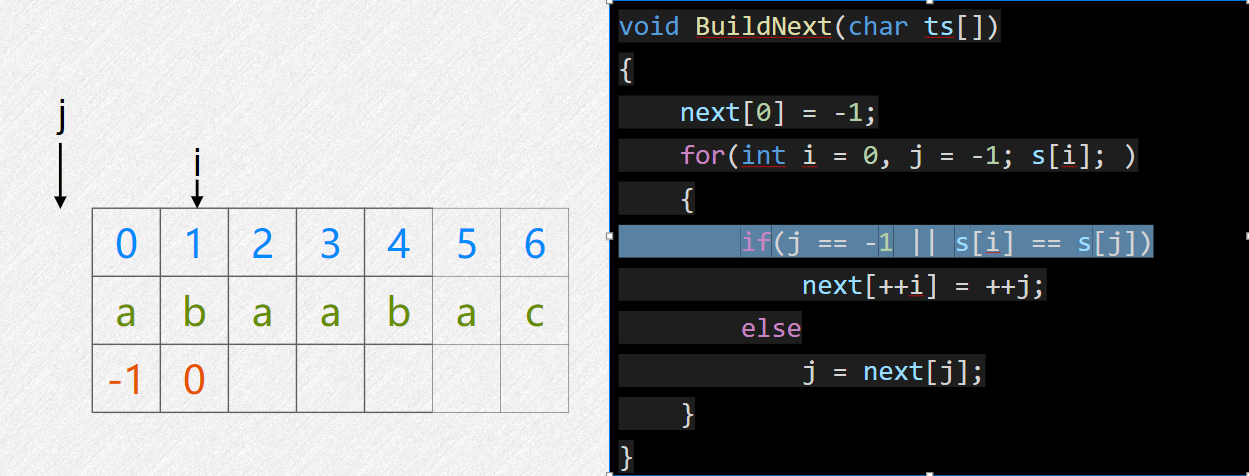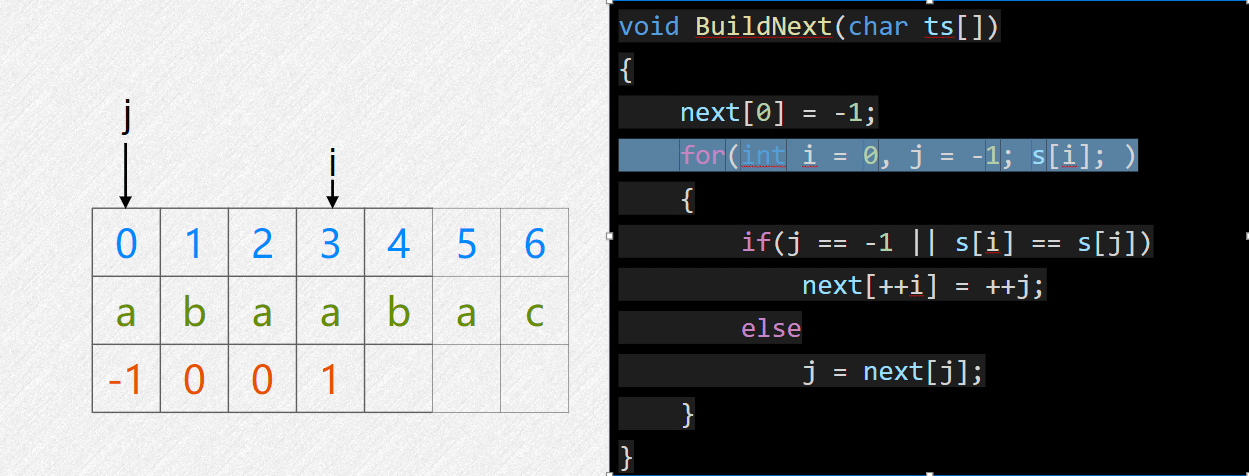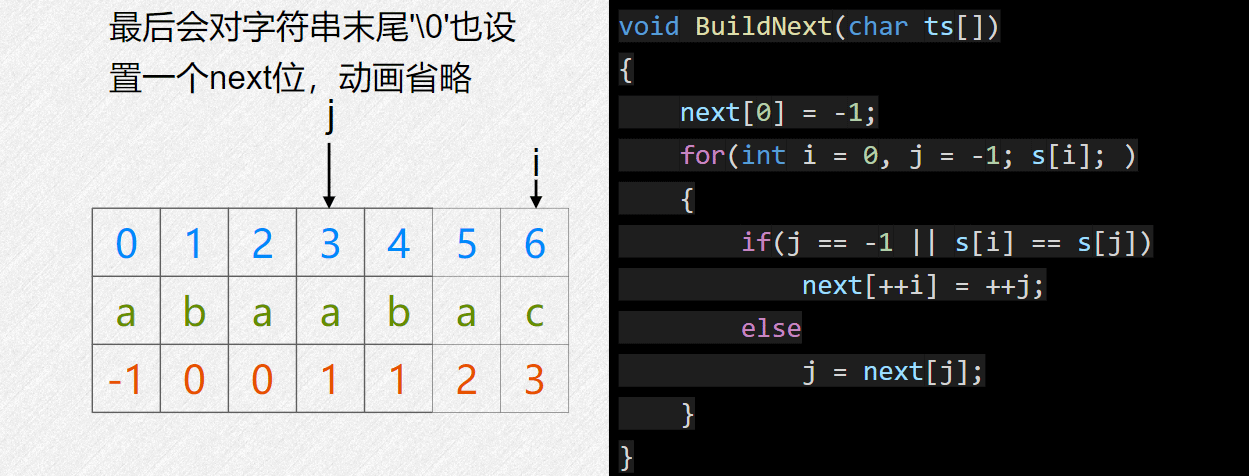
next数组含义： next[i] = j， 表示当从0开始匹配到 i 位置失败时，让 j 挪到 i 当前所对齐的主串位置继续尝试匹配。

计算 next 参考代码， ts 是模式串

int nex[1000];
void BuildNext(char ts[]) {
    nex[0] = -1;
    for(int i = 0, j = -1; ts[i];) {
        if(j == -1 || ts[i] == ts[j])
            nex[++i] = ++j;
        else
            j = nex[j];
    }
}

基于 next 进行匹配，即在 ms 里找 ts 出现的位置

int KmpMatch(char ms[], char ts[]) {
    int tlen = strlen(ts);
    for(int i = 0, j = 0; ms[i];) {
        if(j == -1 || ms[i] == ts[j]) {
            if(j == tlen - 1) {
                // 确认一次完整匹配，此处可支持各类操作
                // 记录位置、统计次数 返回第一次匹配位置等。
                return i - tlen + 1;
            }
            else i ++, j ++;
        }
        else j = nex[j];
    }
    return -1;
}

例：最短循环节

给出 \(s_{1}\)，猜一个最短的 \(s_{2}\)，使 \(s_{2}\) 能以至少重复 \(2\) 次地重复连接得到 \(s_{1}\)，求 \(s_{2}\) 最短长度。

分析：KMP 的 next 能够标记任意前缀的"最长相等前后缀"，如果字符串是循环构成的，那么这个最长相等前后缀的前缀就会覆盖到最后一次循环前，总长度减去这个前缀长度，就是最短的循环节。点击查看详细的（尝试）证明

参考代码

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<string>
#include<unordered_map>
using namespace std;
const int maxs = 1e6 + 10;
int n;
char ts[maxs];
int nex[maxs];

void BuildNex(char ts[], int nex[])
{
    nex[0] = -1;
    for(int i = 0, j = -1; ts[i]; ) {
        if(j == -1 || ts[i] == ts[j])
            nex[++i] = ++j;
        else
            j = nex[j];
    }
}
int main()
{
    int len;
    while(scanf("%d%s", &len, ts) != EOF) {
        BuildNex(ts, nex);
        printf("%d\n", len - nex[len]);
    }
    return 0;
}

AC自动机

回顾 Trie：构建字符范围（比如26个字母）的多叉树，将字符串像查字典一样插入多叉树，查询也是一样，可以作为字符串的哈希方案。

1. 给n个单词，和1个长单词，求有多少个单词是这个长单词的前缀 —— 用 n 个单词建字典树，节点统计单词个数，长单词去匹配，路径上个数求和
2. 给n个单词，和1个短单词，求这个短单词是多少个单词的前缀 —— 用 n 个单词建字典树，节点统计单词个数，短单词匹配成功的节点个数为答案
3. 给两种语言单词对照表，输入任意单词，输出对照另一个语言的单词

KMP：找 \(1\) 个模式串在 \(1\) 个文本中出现的位置

思考： \(n\) 个模式串在 \(1\) 个文本中出现的位置，怎么办？建 \(n\) 个 next 数组然后遍历搞？让模式串每个后缀（即从不同位置开始）在字典树上匹配一遍？都太慢了。

1. 将 \(n\) 个模式串放入Trie
2. 在 Trie 上构建"next数组"——真谛是失配指针——在Trie上匹配失败时，也可以记录一个"下次从哪里开始匹配"

这就是AC自动机的基本思想。

每个节点\(A\)的 fail 指针指向另一个节点\(B\)，\(B\)节点代表的前缀是\(A\)节点前缀的最长后缀。比如从跟节点来到 \(A\) 节点是 "abcde"，其中\(A\) 节点存的是 'e'，\(A\) 的适配指针指向另一个保存 'e' 的节点\(B\)，从根节点到\(B\)的路径可能就会是 "bcde" 或者 "cde" ，具体如何要看模式串集合是否包含有 "bcde" 或 "cde" 这样的前缀的字符串。

构建过程：

1. 根节点的子节点的 fail 指向根
2. BFS 遍历每个节点，为其所有子节点设置 fail 指针
   • 若父节点的 fail 有相同字符的子节点，则指向该子节点
   • 否则递归跳转父节点的 fail，直到找到或回到根

匹配过程：

1. 从根节点开始，按文本字符转移
2. 每次转移后，检查当前节点及其 fail 链上的节点是否为模式串结尾
3. 统计所有匹配的模式串

复杂度：

• 构建：\(O (所有模式串长度之和 + 字符集大小 \times 节点数)\)
• 匹配：\(O (文本长度 + 匹配数)\)

例：出现最多的模式串

给一系列模式串，和一个长文本，求长文本中出现最多的模式串。

方案：构建AC自动机，对每一次匹配到的位置，都沿着失配指针遍历一遍直到根，路径上所有完整单词都计入匹配。最后根据统计结果输出。

#include<cstdio>
#include<queue>
#include<vector>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<functional>
typedef std::pair<int, int> pii;
const int maxn = 1e5;
const int maxm = 1e6 + 10;
struct Trie {
    int ch[26];
    int fail;
    int end;
};
Trie tr[maxn];
int n, tp;
char st[211][111];
char buf[maxm];
const int ROOT = 0;

void Insert(char s[], int idx) {
    int p = ROOT;
    for(int i = 0; s[i]; i ++) {
        int c = s[i] - 'a';
        if(tr[p].ch[c] == -1) {
            tr[p].ch[c] = tp ++;
        }
        p = tr[p].ch[c];
    }
    tr[p].end = idx;        // 记录这是第 idx 个字符串的结束点
}

void BuildFail() {
    std::queue<int> q;
    // 根节点的子节点fail指向根
    for(int i = 0; i < 26; i ++) {
        if(tr[ROOT].ch[i] != -1) {
            tr[tr[ROOT].ch[i]].fail = 0;
            q.push(tr[ROOT].ch[i]);
        }
    }
    
    // BFS遍历每个节点,为其子节点设置fail指针
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        
        // 遍历所有可能的子节点
        for(int i = 0; i < 26; i ++) {
            if(tr[u].ch[i] != -1) {
                int v = tr[u].ch[i];    // 当前节点的子节点
                int f = tr[u].fail;     // 当前节点的fail节点
                
                // 沿着fail指针找到对应字符的转移
                while(f != ROOT && tr[f].ch[i] == -1) {
                    f = tr[f].fail;
                }
                
                // 找到转移或到达根节点
                if(tr[f].ch[i] != -1) {
                    tr[v].fail = tr[f].ch[i];
                } else {
                    tr[v].fail = ROOT;
                }
                
                q.push(v);
            }
        }
    }
}

// 在文本串中查找所有模式串的出现次数
void FindMaxPatterns(char text[]) {
    int len = strlen(text);
    std::vector<pii> cnt(n, {0, 0});  // 记录每个模式串出现次数
    
    // 从根节点开始匹配
    int p = ROOT;
    for(int i = 0; i < len; i++) {
        int c = text[i] - 'a';
        
        // 沿着fail指针找到可以转移的位置
        while(p != ROOT && tr[p].ch[c] == -1) {
            p = tr[p].fail; 
        }
        
        // 找到转移或到达根节点
        if(tr[p].ch[c] != -1) {
            p = tr[p].ch[c];
        }
        
        // 统计当前位置及fail链上所有模式串
        for(int t = p; t != ROOT; t = tr[t].fail) {
            if(tr[t].end != -1) {
                cnt[tr[t].end].first ++;    // 统计匹配成功次数
                cnt[tr[t].end].second = tr[t].end;  // 模式串序号
            }
        }
    }
    // 找出最大出现次数
    std::sort(cnt.begin(), cnt.end(), [](const pii &a, const pii &b) {
        return a.first > b.first || (a.first == b.first && a.second < b.second);
    });
    printf("%d\n", cnt[0].first);
    for(int i = 0; cnt[i].first == cnt[0].first; i ++) {
        printf("%s\n", st[cnt[i].second]);
    }
}

int main() {
    while(scanf("%d", &n) != EOF && n) {
        tp = 1;
        memset(tr, -1, sizeof(tr));
        for(int i = 0; i < n; i ++) {
            scanf("%s", st[i]);
            Insert(st[i], i);    // 插入字典树
        }
        BuildFail();        // 构建失配指针
        
        scanf("%s", buf);
        
        // 查找模式串
        FindMaxPatterns(buf);
    }
    return 0;
}

最小表示法

当字符串 \(S\) 中可以选定一个位置 \(i\) 满足

\[S[i\cdots n]+S[1\cdots i-1]=T\]

则称 \(S\) 与 \(T\) 循环同构

例如 abcdefg 与 efgabcd 是循环同构的，循环左移或循环右移能得到另一个字符串。

最小表示即字符串 \(S\) 循环同构的所有字符串中字典序最小的字符串。

例：判断两字符串是否循环同构

个两个字符串 \(s_{1}\) 和 \(s_{2}\) 判断是否循环同构，字符串长度为 \(n\)

基本暴力：枚举 \(s_{2}\) 的所有循环起点与 \(s_{1}\) 比较，\(O(n^2)\)

改进思路：两个 \(s_{1}\) 拼接形成一个二倍长度的字符串 \(u=s_{1}+s_{1}\)，让 \(s_{2}\) 在 \(u\) 上做 KMP，\(O(n)\)，但对于这个题来说， KMP 有点杀鸡用牛刀。

最小表示思路：比较两个字符串的最小表示的串是否相等。

一个字符串的最小表示计算方法：

1. 初始化 i=0, j=1，考察 i 开始的循环串和 j 开始的循环串的匹配长度 k
2. 当 s[i + k] > s[j + k]，可将 i 跳到 i + k + 1 进行下一轮比较
3. 直到遍历结束，输出 i 与 j 较小的那个

分析第 2 步可以跳到 i + k + 1 的原因：最小表示是要找字典序最小的循环串，i 跳到 i + (p = 1 ~ k) 的位置没有必要，因为至少有 j + (p = 1 ~ k) 的循环串的字典序比它小，即 j+p ~ j+k-1 与 i+p ~ i+k-1 一一对应相等，而s[i + k] > s[j + k]，从而 i 跳到 i + (p<=k) 的位置一定得不到字典序最小的循环串。

参考代码

int k = 0, i = 0, j = 1;
while (k < n && i < n && j < n) {
    if (s[(i + k) % n] == s[(j + k) % n]) {
            k++;
    } else {
        if(s[(i + k) % n] > s[(j + k) % n]) {
            i = i + k + 1;
        } else {
            j = j + k + 1;
        }
        if (i == j) i++;    // i 和 j 不能重叠
        k = 0;
    }
}
i = min(i, j);              // 得到最小循环串的起始位置，即最小表示