32.平衡树

发表于 更新于 分类于 ，

平衡树

本章介绍平衡树的概念，详细讲解 AVL 树的平衡因子、四种平衡旋转操作及代码实现，并简介红黑树、Treap、SBT、B 树和 B + 树等其他平衡树。特别介绍了一种特殊的平衡树——伸展树的基本结构、核心操作、基本操作、序列操作、时间复杂度等内容。

平衡树概念与AVL

回顾二叉排序（查找）树

  • 若其左子树非空，则左子树上所有结点的值均小于根结点的值
  • 若其右子树非空，则右子树上所有结点的值均大于等于根结点的值
  • 其左右子树本身又各是一棵二叉排序树

中序遍历二叉排序树后的结果有什么规律？

AVL树是最先发明的自平衡二叉查找树

二叉排序树的操作－删除

  • 如果所删结点 \(now\) 左右子树有空树：用非空子树树根 \(nex\) 顶替被删结点
  • 否则用左子树中序最末结点 \(nex\) 顶替被删节点 \(now\)，并对 \(nex\) 再次执行删除操作

平衡树

二叉排序树在退化情况下查找与插入性能降低，接近线性而不再是 \(logn\)

\(ASL\)(Average Search Length)：平均搜索长度

在插入删除的过程中动态调整二叉树的姿态，尽可能保持任意子树的左右子树高度一致，即平衡树。

AVL

AVL树是最先发明的自平衡二叉查找树，基于平衡因子实现

  • 平衡因子：该结点左子树与右子树的高度差
  • AVL树任一结点的平衡因子只能取：-1、0 或 1
  • 对于一棵有n个结点的AVL树，其高度和ASL都保持在\(O(log2n)\)

判断下面两个树是否是 AVL

重要操作

平衡旋转：

在插入新节点时，需要调整树的结构以保持平衡。主要有以下四种情况：

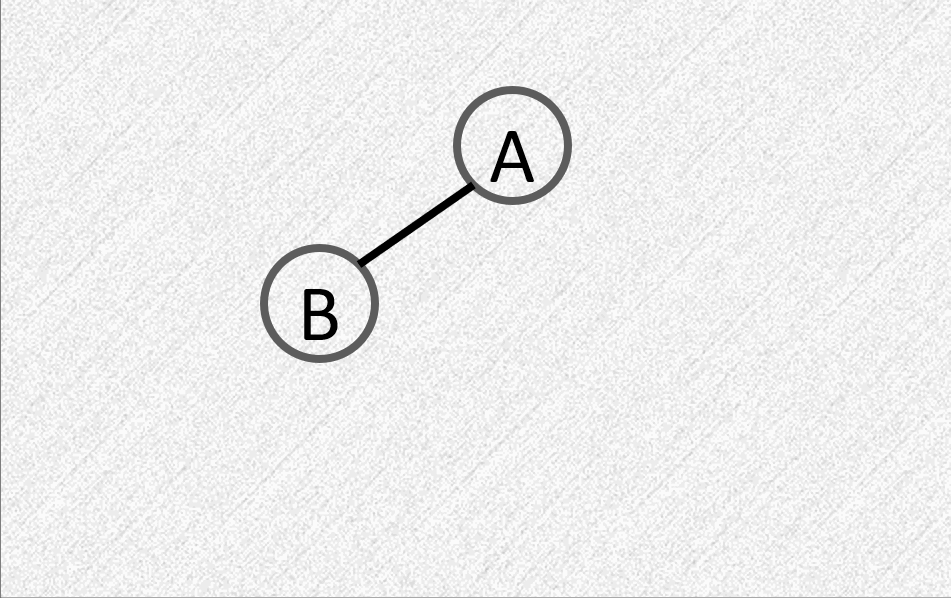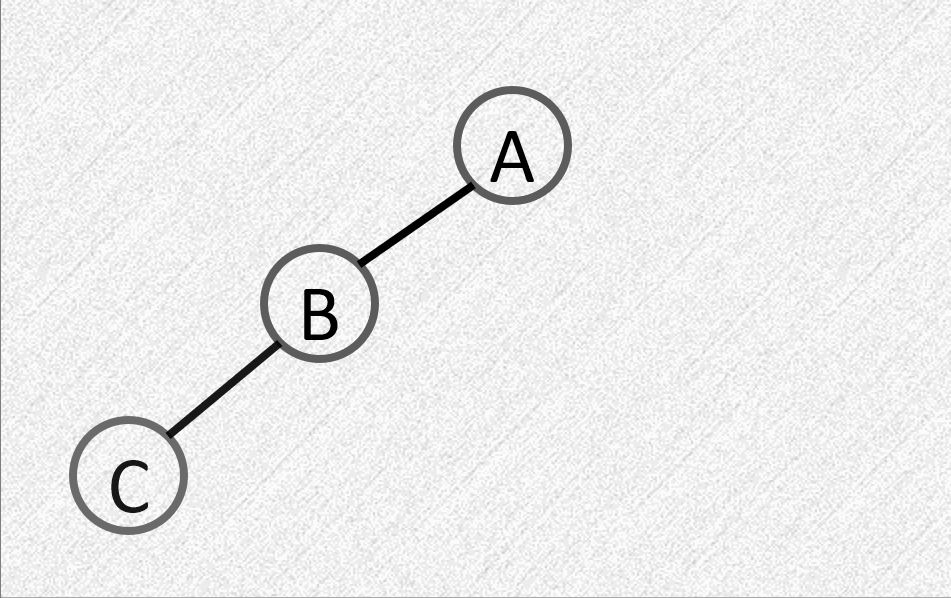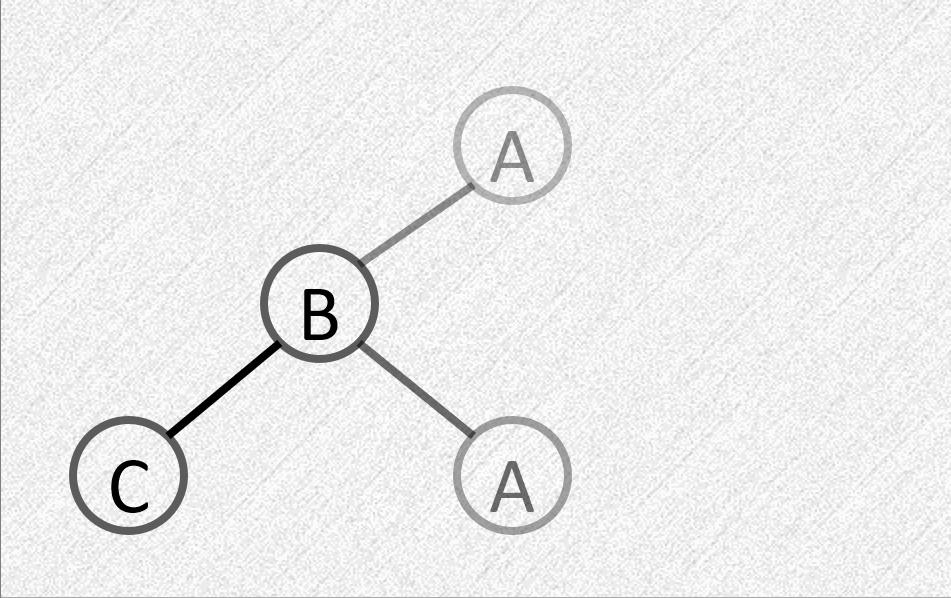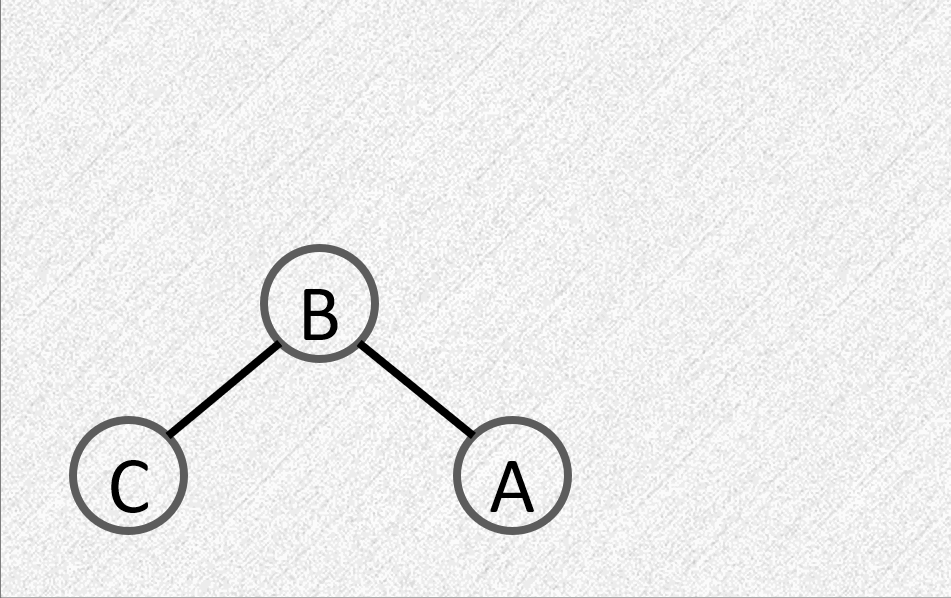
  1. LL：在左子树的左子树插入节点
    • 平衡因子由 \(1\) 变为 \(2\)
    • 需要进行顺时针旋转
  1. RR：在右子树的右子树插入节点
    • 平衡因子由 \(-1\) 变为 \(-2\)
    • 需要进行逆时针旋转
  1. LR：在左子树的右子树插入节点
    • 平衡因子由 \(1\) 变为 \(2\)
    • 需要先对左子树逆时针旋转，再对根顺时针旋转
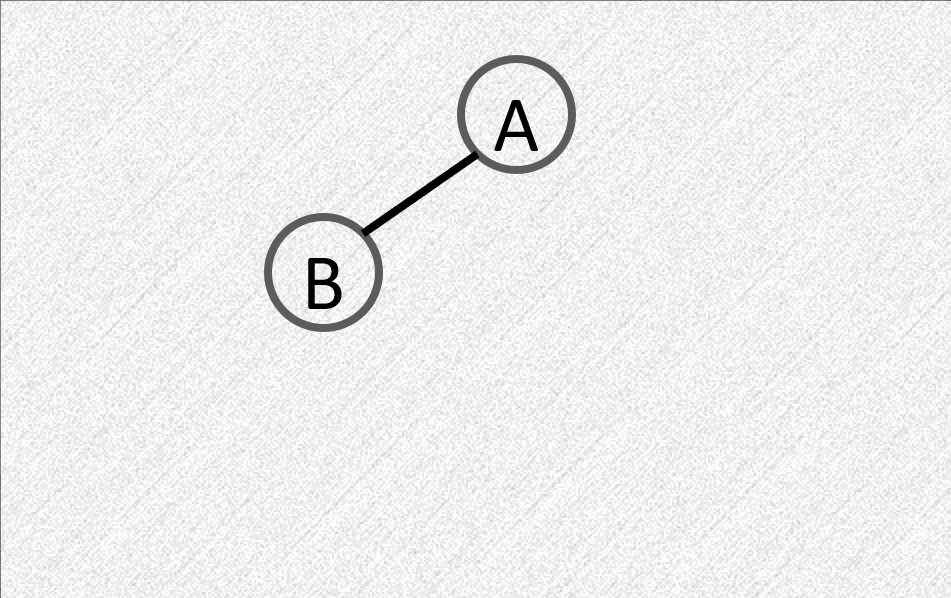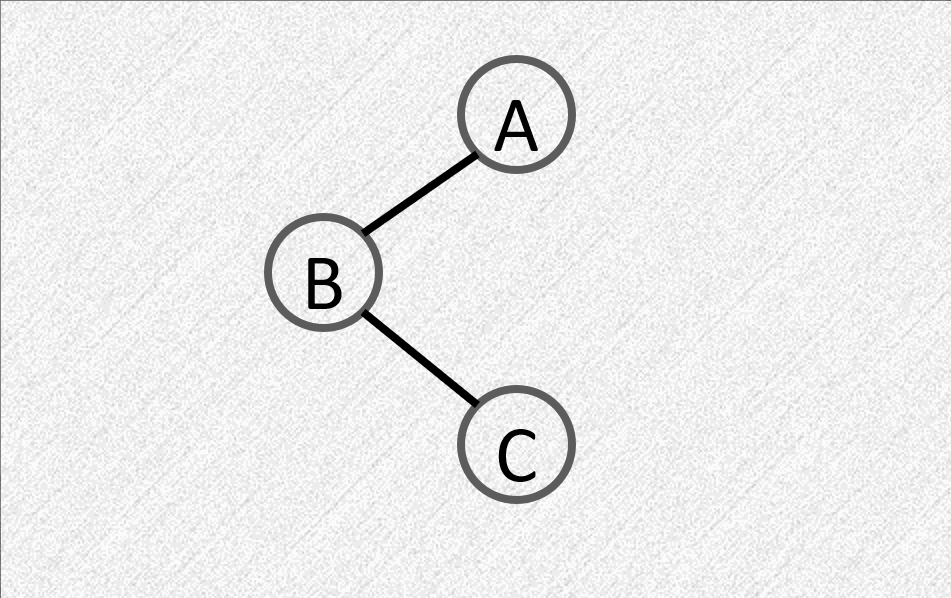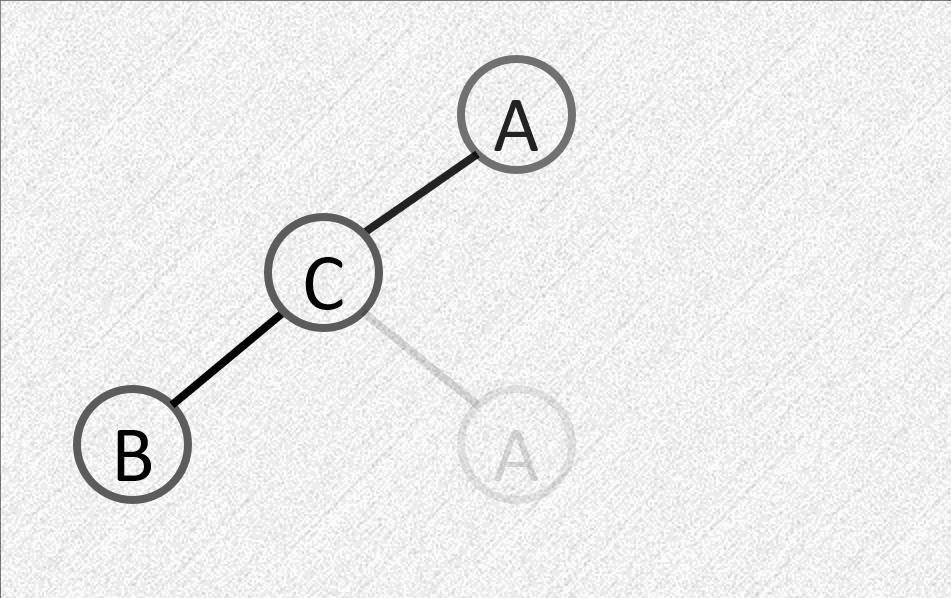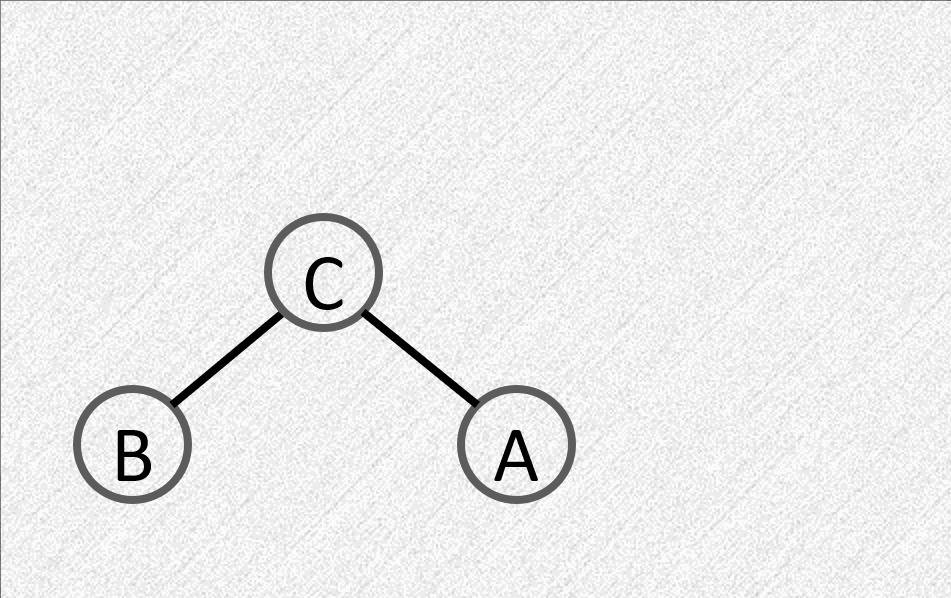
  1. RL：在右子树的左子树插入节点
    • 平衡因子由 \(-1\) 变为 \(-2\)
    • 需要先对右子树顺时针旋转，再对根逆时针旋转

参考模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
/*
注释内容由AI生成，仅供参考
*/
const int maxn = 1e5 + 10;                    // 定义最大节点数

struct Node {                                  // 定义AVL树节点结构
    int key;                                   // 键，用于二叉树排序
    int data;                                  // 数据域，不参与排序的数据
    int left;                                  // 左子树指针
    int right;                                 // 右子树指针
    int height;                                // 节点高度
    void Init(){data = key = left = right = height = -1;}           // 初始化节点
    void Init(int k_, int d_=0){Init(); key = k_; data = d_;}       // 带参数初始化
    Node(){Init();}                            // 默认构造函数
    Node(int k_, int d_=0){Init(k_, d_);}      // 带参数构造函数
};

Node tr[maxn];                                // 节点数组
int root, tp;                                 // root为根节点，tp为内存分配指针

inline int UpdateHeight(int now) {            // 更新节点高度
    int lh = tr[now].left == -1 ? 0 : tr[tr[now].left].height;     // 获取左子树高度
    int rh = tr[now].right == -1 ? 0 : tr[tr[now].right].height;   // 获取右子树高度
    return tr[now].height = (lh > rh ? lh : rh) + 1;               // 更新当前节点高度
}

inline int HeightDiff(int now) {              // 计算平衡因子
    int lh = tr[now].left == -1 ? 0 : tr[tr[now].left].height;     // 获取左子树高度
    int rh = tr[now].right == -1 ? 0 : tr[tr[now].right].height;   // 获取右子树高度
    return lh - rh;                           // 返回平衡因子（左子树高度 - 右子树高度）
}

int LL(int an) {                              // LL型旋转（顺时针旋转）
    int bn = tr[an].left;                     // 保存左子节点
    int dn = tr[bn].right;                    // 保存左子节点的右子树
    tr[bn].right = an;                        // 调整指针关系
    tr[an].left = dn;
    UpdateHeight(an);                         // 更新高度
    UpdateHeight(bn);
    return bn;                                // 返回新的根节点
}

int RR(int an) {                              // RR型旋转（逆时针旋转）
    int bn = tr[an].right;                    // 保存右子节点
    int dn = tr[bn].left;                     // 保存右子节点的左子树
    tr[bn].left = an;                         // 调整指针关系
    tr[an].right = dn;
    UpdateHeight(an);                         // 更新高度
    UpdateHeight(bn);
    return bn;                                // 返回新的根节点
}

int LR(int an) {                              // LR型旋转（先逆时针后顺时针）
    tr[an].left = RR(tr[an].left);           // 先对左子树进行逆时针旋转
    return LL(an);                            // 再对根节点进行顺时针旋转
}

int RL(int an) {                              // RL型旋转（先顺时针后逆时针）
    tr[an].right = LL(tr[an].right);         // 先对右子树进行顺时针旋转
    return RR(an);                            // 再对根节点进行逆时针旋转
}

void Insert(int &now, int key, int data=0) {  // 插入节点
    if(now == -1) {                           // 如果当前节点为空
        now = tp ++;                          // 分配新节点
        tr[now].Init(key, data);              // 初始化新节点
    }
    else if(key < tr[now].key) {              // 如果键值小于当前节点
        Insert(tr[now].left, key, data);      // 递归插入左子树
        if(HeightDiff(now) == 2)              // 如果平衡因子为2
            now = key < tr[tr[now].left].key ? // 判断是LL还是LR型
                LL(now) : LR(now);            // 进行相应的旋转
    }
    else if(key > tr[now].key) {              // 如果键值大于当前节点
        Insert(tr[now].right, key, data);     // 递归插入右子树
        if(HeightDiff(now) == -2)             // 如果平衡因子为-2
            now = key > tr[tr[now].right].key ? // 判断是RR还是RL型
                RR(now) : RL(now);            // 进行相应的旋转
    }
    UpdateHeight(now);                        // 更新当前节点高度
}

void Delete(int &now, int key) {              // 删除节点
    if(now == -1) return;                     // 如果节点为空，直接返回
    else if(key < tr[now].key) {              // 如果键值小于当前节点
        Delete(tr[now].left, key);            // 递归删除左子树
    }
    else if(key > tr[now].key) {              // 如果键值大于当前节点
        Delete(tr[now].right, key);           // 递归删除右子树
    }
    else {                                    // 找到要删除的节点
        if(tr[now].left == -1) {              // 如果左子树为空
            now = tr[now].right;              // 用右子树替代
        }
        else if(tr[now].right == -1) {        // 如果右子树为空
            now = tr[now].left;               // 用左子树替代
        }
        else {                                // 如果左右子树都不为空
            int nd;                           // 找到左子树中的最大值
            for(nd = tr[now].left; ; nd = tr[nd].right)
                if(tr[nd].right == -1) break;
            tr[now].key = tr[nd].key;         // 用最大值替代当前节点
            tr[now].data = tr[nd].data;
            Delete(tr[now].left, tr[nd].key); // 递归删除最大值节点
        }
    }
    if(now == -1) return;                     // 如果节点为空，直接返回
    UpdateHeight(now);                        // 更新当前节点高度
    if(HeightDiff(now) == 2) {                // 如果平衡因子为2
        now = HeightDiff(tr[now].left) >= 0 ? // 判断是LL还是LR型
            LL(now) : LR(now);                // 进行相应的旋转
    }
    else if(HeightDiff(now) == -2) {          // 如果平衡因子为-2
        now = HeightDiff(tr[now].right) <= 0 ? // 判断是RR还是RL型
            RR(now) : RL(now);                // 进行相应的旋转
    }
}

其它各种平衡树简介

红黑树

红黑树是一种广泛使用的平衡树,它通过节点的颜色来维持平衡:

  1. 每个节点要么是红色,要么是黑色
  2. 根节点是黑色
  3. 叶子节点(NIL)是黑色
  4. 如果一个节点是红色,则它的子节点必须是黑色
  5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

相比AVL树,红黑树: - 牺牲了部分平衡性来换取更少的旋转操作 - 插入删除的维护成本更低 - 被广泛应用于标准库实现中(如C++ STL)

Treap

Treap = Tree + Heap,是一种随机化的平衡二叉树:

  1. 每个节点除了键值外还随机分配一个优先级
  2. 按照键值组成二叉搜索树
  3. 按照优先级组成最大堆
  4. 通过旋转操作来维护堆的性质
  5. 期望的高度是O(log n)

SBT (Size Balanced Tree)

SBT是由ICPC选手陈启峰发明的一种平衡树:

  1. 通过维护子树大小(size)而不是高度来保持平衡
  2. 平衡条件比较简单:较小子树的大小不小于较大子树的子树大小
  3. 实现相对简单,只需要维护size信息
  4. 各种操作的时间复杂度都是O(log n)
  5. 在某些情况下比红黑树更容易实现和维护

B树和B+树

这两种树主要用于数据库和文件系统:

  1. 允许每个节点包含多个键值
  2. 所有叶子节点都在同一层
  3. B+树的非叶节点只存储键值,数据都存在叶子节点
  4. 特别适合磁盘等外存储器的存储方式
  5. 广泛应用于数据库索引和文件系统中

用STL解决简单平衡树问题

一些只需要利用平衡树性质，但没有细化考查的问题，可以用STL的map或set完成。

std::map 由红黑树实现的数据有序，所有的“键”插入后都是有序的，比如可以用 lower_bound 找特定键的前驱

1
2
3
4
5
6
7
8
9
std::map<int, int> myMap;
// 假设 myMap 已经填充了一些数据
auto predecessorIt = myMap.lower_bound(targetKey);
if (predecessorIt != myMap.begin()) {
    // 回退一步得到前驱
    --predecessorIt;
} else {
    // 没有前驱
}

std::set 是集合的概念，相对map来说它只有“键”没有“值”，在不需要数据映射的时候用 set 更简洁，比如找一个键的前驱

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <iostream>
#include <set>

int main() {
    std::set<int> mySet = {1, 3, 5, 7, 9};
    int target = 5;
    
    auto successorIt = mySet.upper_bound(target);
    if (successorIt != mySet.end()) {
        std::cout << "Successor: " << *successorIt << std::endl;
    } else {
        std::cout << "No successor found." << std::endl;
    }
}

map和set 都是平衡树实现，在简单场景中可以不用繁琐地自己去实现平衡树，在比赛中节约大量时间。

伸展树（Splay）

伸展树通过"伸展"操作将最近访问的节点移动到根节点，从而保证树的高度在均摊意义下为\(O(log n)\)。

传统平衡树的操作，伸展树基本都可以完成，但可能复杂度高一些，非特异需求不建议用伸展树。

除传统平衡树支持的操作外，伸展树更擅长执行以下操作:

  1. 区间操作：通过将区间两端点伸展到根节点附近，可以方便地进行区间修改和查询
  2. 最近访问优化：由于最近访问的节点会被移动到根部，对于有局部性的访问模式效率更高
  3. 动态统计：可以方便地维护子树信息，适合需要频繁修改和查询统计信息的场景
  4. 序列操作：通过中序遍历性质，可以方便地进行序列的分割、合并等操作

所以掌握一种传统平衡树（比如AVL或SBT）外，还应当掌握伸展树的使用。

基本结构

伸展树的基本结构包含以下信息：

1
2
3
4
5
6
7
8
9
10
11
12
13
struct SplayNode {
    int ch[2];    // 左右儿子
    int fa;       // 父亲节点
    int val;      // 节点值
    int cnt;      // 值出现次数
    int sz;       // 子树大小
    int lz;       // 懒标记(用于区间操作)
    
    void Init() {
        ch[0] = ch[1] = fa = val = cnt = sz = lz = 0;
    }
    SplayNode() { Init(); }
};

每个节点需要维护以下信息：

  • ch[2]：存储左右子节点的编号
  • fa：存储父节点的编号
  • val：节点的值
  • cnt：该值出现的次数
  • sz：以该节点为根的子树大小
  • lz：用于区间操作的懒标记

核心操作

1. 旋转操作

旋转是Splay树的基础操作，用于将一个节点上移一层。旋转操作需要保证：

  1. 不破坏二叉查找树的性质
  2. 正确维护父子关系
  3. 更新节点信息

旋转分为两种情况：

  • 当节点是其父节点的左儿子时，进行右旋
  • 当节点是其父节点的右儿子时，进行左旋
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void Rotate(int x) {
    int y = sn[x].fa, z = sn[y].fa;
    int chk = Ws(x);  // 判断x是y的左儿子还是右儿子
    
    // 更新y的子节点
    sn[y].ch[chk] = sn[x].ch[chk ^ 1];
    if(sn[y].ch[chk]) 
        sn[sn[y].ch[chk]].fa = y;
        
    // 更新x和y的关系
    sn[x].ch[chk ^ 1] = y;
    sn[y].fa = x;
    
    // 更新x和z的关系
    sn[x].fa = z;
    if(z) 
        sn[z].ch[y == sn[z].ch[1]] = x;
        
    // 维护节点信息
    Maintain(y);
    Maintain(x);
}

2. 伸展操作

伸展操作是Splay树的核心，它将一个节点通过一系列旋转移动到根节点。伸展操作分为三种情况：

  1. zig：当父节点是根节点时，直接旋转
  2. zig-zig：当节点和父节点都是左儿子或都是右儿子时，先旋转父节点，再旋转当前节点
  3. zig-zag：当节点和父节点一个是左儿子一个是右儿子时，连续旋转两次当前节点
1
2
3
4
5
6
void Splay(int x, int target=0) {
    for(int y = sn[x].fa; (y = sn[x].fa) != target; Rotate(x))
        if(sn[y].fa != target) 
            Rotate(Ws(x) == Ws(y) ? y : x);
    if(!target) rt = x;
}

基本操作

插入操作

插入操作的基本步骤：

  1. 如果树为空，直接创建新节点作为根节点
  2. 否则，按照二叉查找树的性质找到插入位置
  3. 如果找到相同值的节点，增加计数
  4. 否则创建新节点
  5. 最后进行伸展操作，将新节点移到根节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void Insert(int k) {
    if(!rt) {
        rt = Add(k);
        return;
    }
    int cur = rt, f = 0;
    while(true) {
        if(sn[cur].val == k) {
            sn[cur].cnt++;
            Maintain(cur);
            Maintain(f);
            Splay(cur);
            break;
        }
        f = cur;
        cur = sn[cur].ch[sn[cur].val < k];
        if(!cur) {
            int nn = Add(k, f);
            Splay(nn);
            break;
        }
    }
}

删除操作

删除操作的基本步骤：

  1. 首先找到要删除的节点并伸展到根
  2. 如果节点计数大于1，直接减少计数
  3. 如果节点没有子节点，直接删除
  4. 如果节点只有一个子节点，用子节点替代
  5. 如果节点有两个子节点，找到前驱节点替代，然后删除前驱节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void Del(int k) {
    Rank(k);
    if(sn[rt].cnt > 1) {
        sn[rt].cnt--;
        Maintain(rt);
        return;
    }
    if(!sn[rt].ch[0] && !sn[rt].ch[1]) {
        Clear(rt);
        rt = 0;
        return;
    }
    // 处理只有一个子节点的情况
    for(int i = 0; i <= 1; i++) {
        if(sn[rt].ch[i]) continue;
        int cur = rt;
        rt = sn[rt].ch[i ^ 1];
        sn[rt].fa = 0;
        Clear(cur);
        return;
    }
    // 处理有两个子节点的情况
    int cur = rt, x = RtPre();
    sn[sn[cur].ch[1]].fa = x;
    sn[x].ch[1] = sn[cur].ch[1];
    Clear(cur);
    Maintain(rt);
}

前驱后继查询

前驱后继查询的基本步骤：

  1. 前驱：找到左子树中的最大值
  2. 后继：找到右子树中的最小值
  3. 查询后将节点伸展到根
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int RtPre(int cur=0) {
    if(!cur) cur = sn[rt].ch[0];
    else cur = sn[cur].ch[0];
    if(!cur) return cur;
    while(sn[cur].ch[1]) cur = sn[cur].ch[1];
    Splay(cur);
    return cur;
}

int RtNxt(int cur=0) {
    if(!cur) cur = sn[rt].ch[1];
    else cur = sn[cur].ch[1];
    if(!cur) return cur;
    while(sn[cur].ch[0]) cur = sn[cur].ch[0];
    Splay(cur);
    return cur;
}

序列操作

Splay树也可以用于维护序列信息。与线段树相比，Splay树虽然常数较大，但支持更复杂的序列操作，如区间翻转等。

将序列建成的Splay树具有以下性质：

  1. 中序遍历相当于原序列从左到右的遍历
  2. 每个节点代表序列中的一个元素
  3. 一棵子树代表序列中的一段区间

区间操作

以区间翻转为例，操作步骤如下：

  1. 将区间左端点前一个节点伸展到根
  2. 将区间右端点后一个节点伸展到根的右儿子
  3. 此时根的右儿子的左子树就是目标区间
  4. 对该子树进行翻转操作并打上懒标记
1
2
3
4
5
6
7
8
9
10
void DFS(int cur, int k) {
    if(!cur) return;
    PushDown(cur);
    DFS(sn[cur].ch[0], k);
    DFS(sn[cur].ch[1], k);
    sn[sn[cur].fa].ch[Ws(cur)] = 0;
    Maintain(sn[cur].fa);
    tbi.push_back(sn[cur].val);
    cct.push_back(sn[cur].cnt);
}

懒标记管理

对于区间操作，需要维护懒标记：

1
2
3
4
5
6
7
8
9
10
11
12
void PushDown(int x) {
    if(!x || !sn[x].lz) return;
    UpdateLz(sn[x].ch[0], sn[x].lz);
    UpdateLz(sn[x].ch[1], sn[x].lz);
    sn[x].lz = 0;
}

void UpdateLz(int x, LL lz) {
    if(!x) return;
    sn[x].lz += lz;
    sn[x].val -= lz;
}

在访问节点时需要下传标记：

1
2
3
4
5
6
7
8
void Splay(int x, int target=0) {
    std::vector<int> path;
    for(int f = x; f; f = sn[f].fa) path.push_back(f);
    for(int i = path.size() - 1; i >= 0; i--) PushDown(path[i]);
    for(int y; (y = sn[x].fa) != target; Rotate(x))
        if(sn[y].fa != target) Rotate(Ws(x) == Ws(y) ? y : x);
    if(!target) rt = x;
}

应用示例

以K小值查询为例，展示了Splay树处理区间操作的能力：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void UpperBound(int k) {
    int lastLager = 0, cur = rt;
    while(cur) {
        PushDown(cur);
        if(k < sn[cur].val) {
            lastLager = cur;
            if(!sn[cur].ch[0]) break;
            cur = sn[cur].ch[0];
        }                
        else {
            if(!sn[cur].ch[1]) break;
            cur = sn[cur].ch[1];
        }
    }
    if(sn[cur].val <= k) cur = lastLager;
    if(cur) Splay(cur);
    return cur;
}

这个例子展示了如何：

  1. 维护区间信息
  2. 处理懒标记
  3. 进行区间查询和修改

通过这些操作，Splay树可以高效地处理各种序列操作问题。

时间复杂度

  • 单次操作均摊复杂度：\(O(log n)\)
  • 空间复杂度：\(O(n)\)