31.图论基础2

发表于 分类于 ，

图论基础2

从网络与流的基本概念出发，讨论最大流问题及其求解算法，包括Ford-Fulkerson方法、Edmonds-Karp算法和Dinic算法。介绍最大流最小割定理，以及费用流问题和二分图匹配问题。

网络与流

网络（流网络，Flow Network）定义：

  • 有向图 \(G=(V,E)\)
  • 每条边 \((u,v)\in E\) 有权值 \(c(u,v)\) 表示容量（物料的最大流速）
  • \((u,v)\notin E\) 时 \(c(u,v)=0\)
  • 有两个特殊的点：源点 \(s\in V\)，汇点 \(t\in V\)

其实就是有向图。

流：\(f(u,v)\) 定义在 \((u\in V, v\in V)\) 上的实数函数且满足：

  • 容量限制：\(f(u,v)\leq c(u,v)\) > 每条边流量不能超过容量
  • 流量守恒：\(\forall u\in V-\{s,t\}\) 有 \(\sum_{v\in V}f(v,u)=\sum_{u\in V}f(u,v)\) > 源点\(s\)流出多少，最终都一定全部流入汇点\(t\)
  • 除源点 \(s\) 和汇点 \(t\) 外，流入节点的总量等于节点流出的总量 > 除源点和汇点外，每个点流入多少就必须流出多少，不会“囤积”
  • "流"的流量：\(|f|=\sum_{v\in V}f(s,v)-\sum_{v\in V}f(v,s)\) > 源点\(s\)总共流出了多少，或者说汇点\(t\)总共流入了多少

多个源点汇点的网络，可以添加超级源点与超级汇点，转换为常规的流网络

最大流

最大流：流网络中符合流的限制条件的 \(|f|\) 最大的流 \(f\)

最大流也是一个线性规划问题：

\(\max |f| = \sum_{v\in V}f(s,v) - \sum_{v\in V}f(v,s)\)

s.t. \(f(i,j) \leq c(i,j)\), \((i,j)\in E\)

\(\sum_{j\in V}f(i,j) = \sum_{j\in V}f(j,i)\), \(i\in V-\{s,t\}\)

\(f(i,j) \geq 0\), \((i,j)\in E\)

\(|f| \geq 0\)

求解线性规划的算法可以解最大流，不过最大流有更有效的方法

Ford-Fulkerson 方法

"方法"而不是"算法"：Ford-Fulkerson有不同的实现方式

先做一个预设：让\(f(u,v)=-f(v,u)\)，即\(u\)流向\(v\)的流量，可以抽象地看作有有个\(v\)流向\(u\)的负流量。

  • 残存网络：\(c_f(u,v)=c(u,v)-f(u,v)\) > 每条边还能增加多少流量
  • 增广路：残存网络中\(s\)到\(t\)的简单路径 > 沿着能增加流量的边，从 \(s\) 走到 \(t\) 的路径，说明这条路径整体可以增加流量
  • 残存容量：增广路上能加推的最大流量 > 这条增广路必然有个边能增加的流量最小，是瓶颈，导致整条路径最多只能增加这么多流量
  • 抵消操作：增广路加推流量时，部分边撤回的原流量 > 把一个边 \(A\rightarrow B\) 的流量“撤回去”，相当于反向边 \(B \rightarrow A\) 的流量增加了

如果残存网络不包含增广路径，那么就无法增加流了，说明已得到最大流

算法设计思路：不断寻找增广路

Edmonds-Karp算法

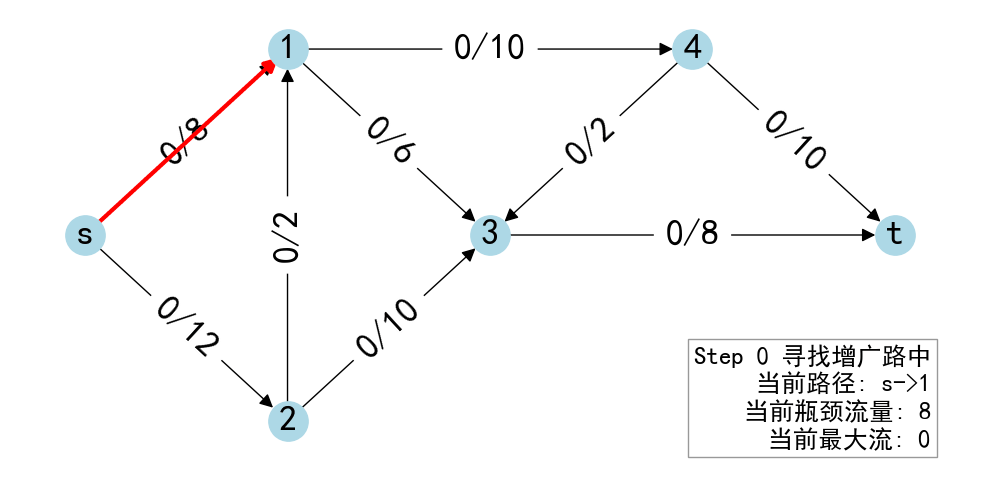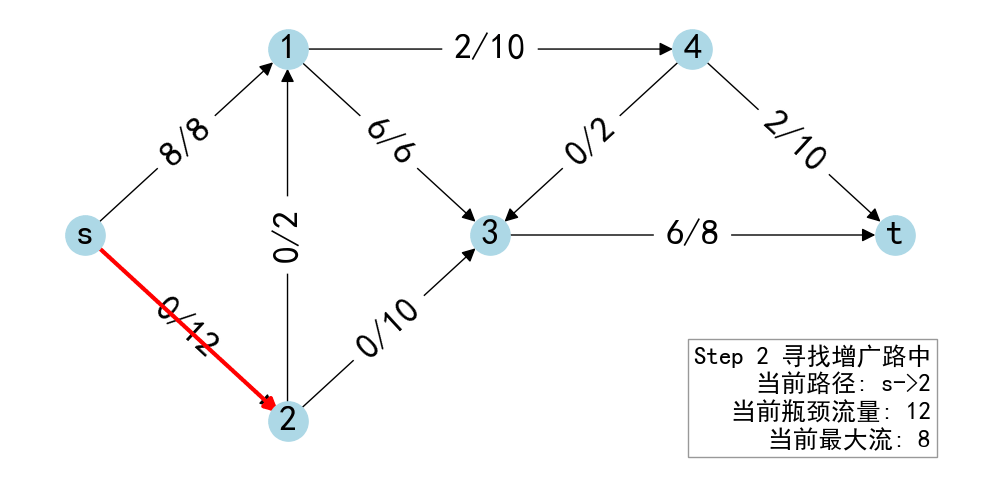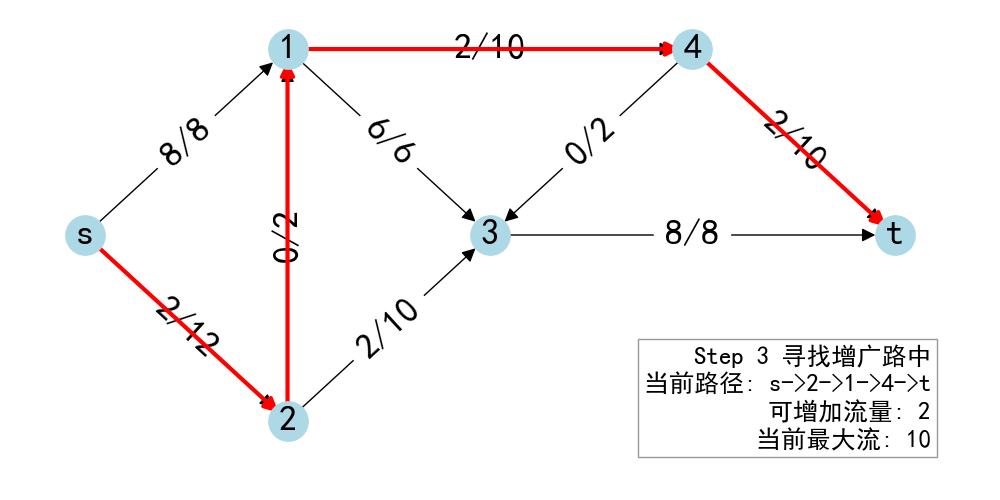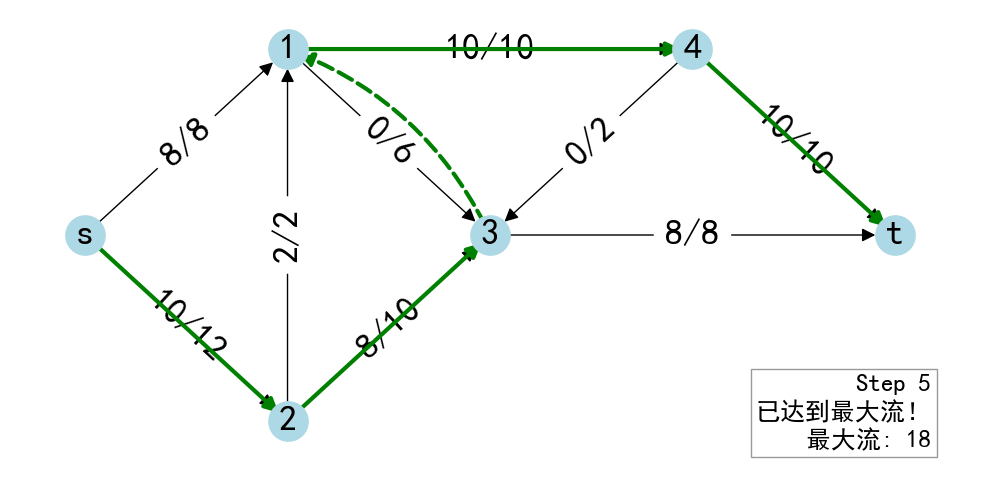
  1. 从\(s\)出发 BFS 找到\(t\)，得到增广路\(p\)
  2. 计算路径各边在残存网络的最小值\(\delta\)
  3. 给\(p\)的每条边加上\(\delta\)的流量
  4. 重复1~4，直到没有增广路

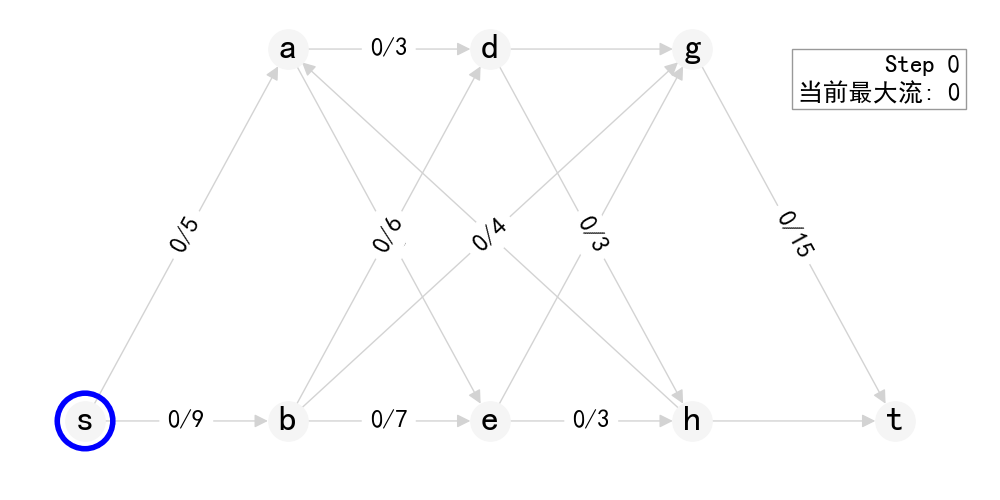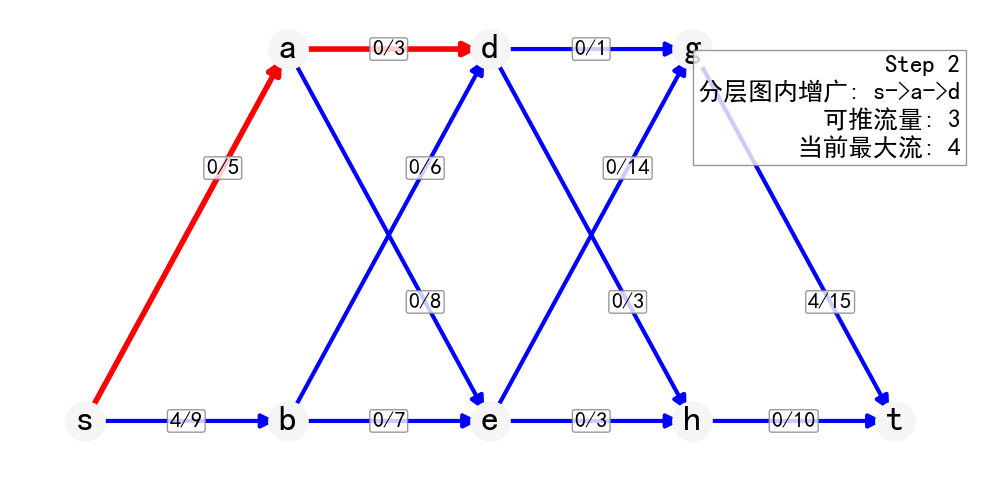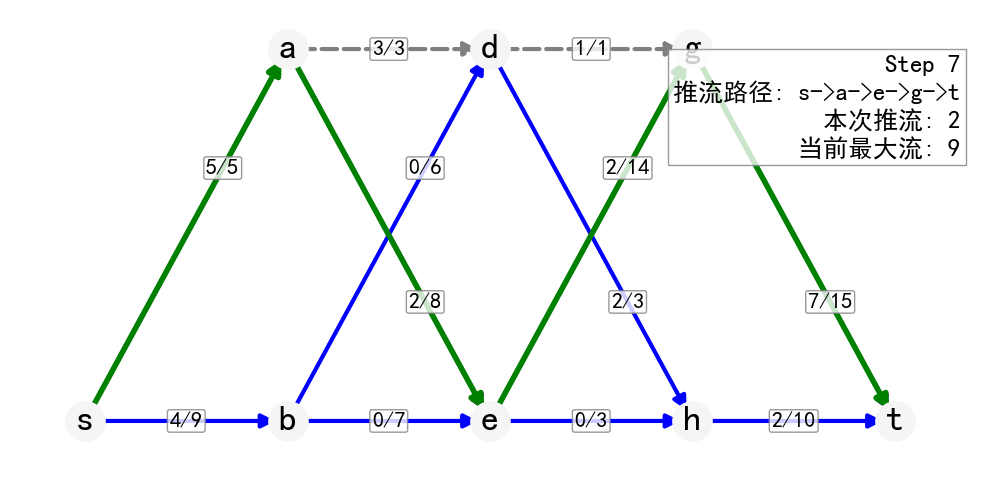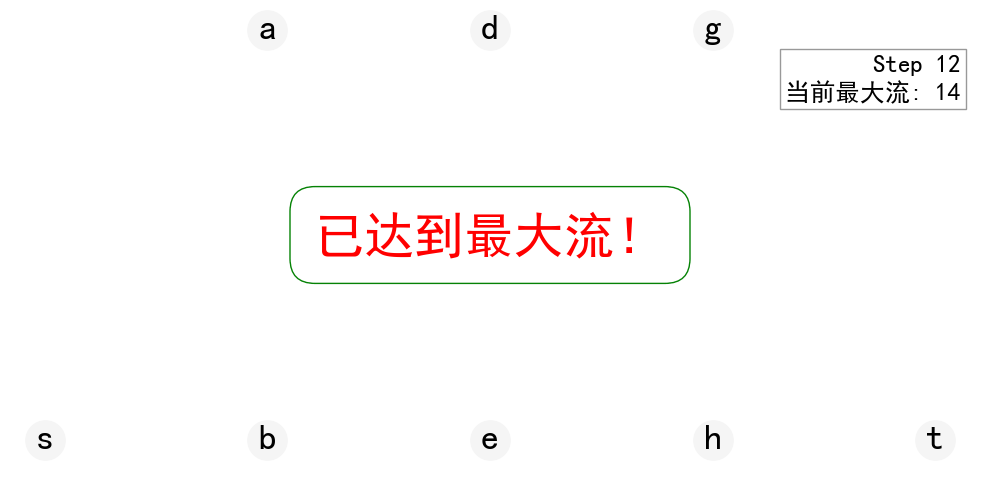
Dinic算法

对残存网络分层：

用BFS根据各节点到 \(s\) 的距离分层，得到残存网络的分层图

分析：

  1. 每次基于BFS的分层网络推流，只会沿着从s到t的最短路径推流。这是因为BFS分层保证了每个节点的层数就是其到源点s的最短距离。
  2. 当一轮推流结束后，原来的最短路径必然会被"堵死"（至少有一条边的残余容量变为0）。否则还可以继续在这条路径上推流，与"一轮结束"矛盾。
  3. 因此下一轮BFS时，s到t的最短路径长度一定会增加。这是因为:
    • 原来的最短路径已经不存在于残存网络中
    • 新的最短路径必然要绕过"堵死"的边，所以路径会更长
  4. 由于图中s到t的路径长度不可能超过节点数n，且每轮至少增加1，所以:
    • 最短路径长度从1开始增长
    • 最多增长到n-1就会终止
    • 总轮数不超过n-1轮
  5. 这保证了算法在有限步内一定会终止，且找到最大流

参考代码

前向星建图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int fst[maxn];  // 每个顶点发出的边的边链表头节点，可初始化为 -1 表示每个顶点都还没有边
int nex[maxm];  // 同个顶点发出的边的边节点 next 域
int v[maxm];    // 边的收入顶点
int cap[maxm];  // 边的容量，同时用作残存网络计算
int tp;         // 分配“内存”的模拟游标
void AddEdge(int a, int b, int w) {
    v[tp] = b;          // 边tp的收入点是b
    cap[tp] = w;        // 容量是w
    nex[tp] = fst[a];   // 头插法为顶点a的边链表插入tp这条边
    fst[a] = tp ++;     // 新增边的游标为tp，之后让tp指向“下一块内存”
}
void DbEdge(int a, int b, int w){
    AddEdge(a, b, w);   // 添加正向边
    AddEdge(b, a, 0);   // 反向边容量为0
}

BFS 建立分层网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int ly[maxn], work[maxn], n, m, so, te;
bool DiBFS() {
    queue<int> q; memset(ly, -1, sizeof(ly));   // 初始化各节点的层
    q.push(so); ly[so] = 0;                     // 源点入队，层为0
    while(!q.empty()) {                         // 开始BFS
        int now = q.front(); q.pop();
        for(int i = fst[now]; i != -1; i = nex[i]) {    // 枚举当前点发出的边
            if(ly[v[i]] >= 0 || !cap[i]) continue;      // 该边收入点已分层或无容量跳过
            ly[v[i]] = ly[now] + 1;                     // 该边收入点为下一层
            if(v[i] == te) return true;                 // 找到汇点可以结束
            q.push(v[i]);                               // 收入点入队继续BFS
        }
    }
    return false;
}

单次DFS推流

1
2
3
4
5
6
7
8
9
10
11
12
13
int DiDFS(int cur, int inc) {
    int tinc;
    if(cur == te) return inc;
    for(int &i = work[cur]; i != -1; i = nex[i]) {      // 遍历cur发出的边，游标work不重置
        if(cap[i] && ly[v[i]] == ly[cur] + 1 &&         // 只沿着层增加方向
            (tinc = DiDFS(v[i], min(inc, cap[i])))){    // 取路径上最小容量
            cap[i] -= tinc;         // 正向边残存网络容量减小
            cap[i ^ 1] += tinc;     // 反向边残存网络容量增加
            return tinc;
        }
    }
    return 0;
}

调用DFS推流在分层图上反复推流直到断开

1
2
3
4
5
6
7
8
int Dinic() {
    int ret = 0, tinc;
    while(DiBFS()) {    // 计算分层图
        for(int i = 0; i <= n; i ++) work[i] = fst[i];  // 初始化工作游标
        while(tinc = DiDFS(so, inf)) ret += tinc;       // DFS推多次流，游标不重置
    }
    return ret;
}

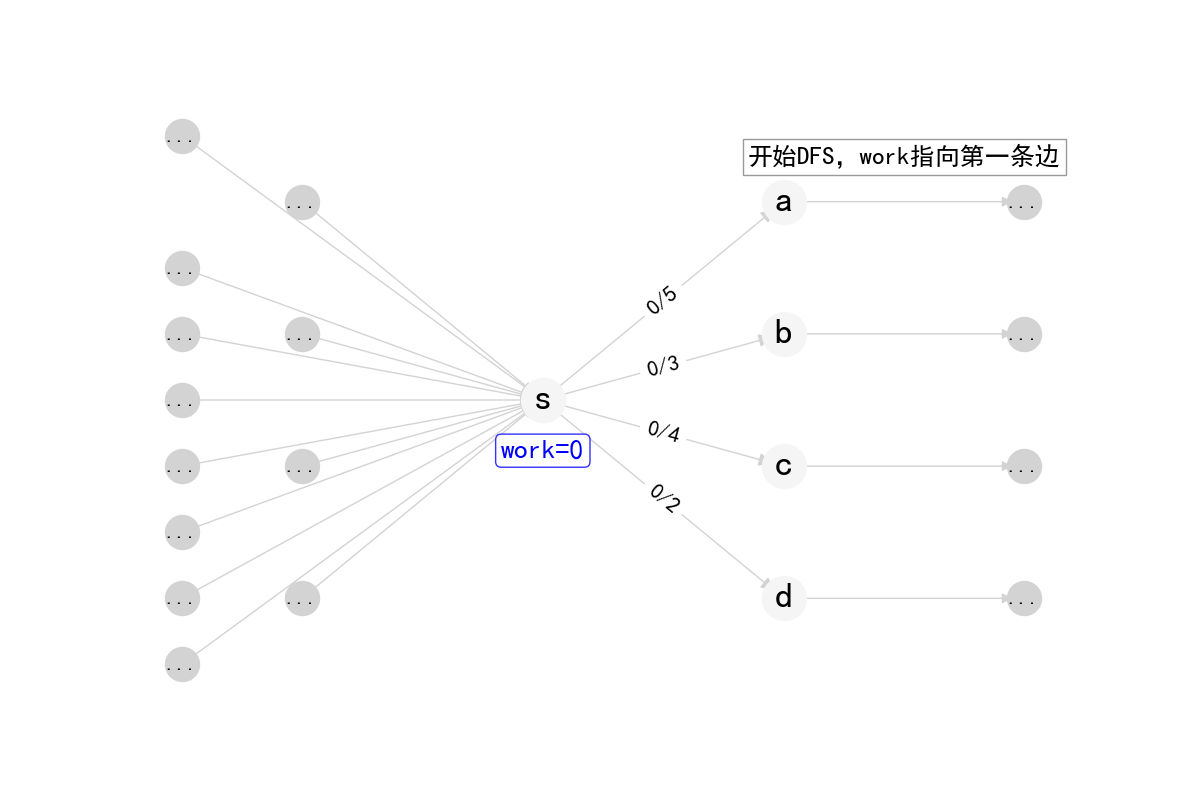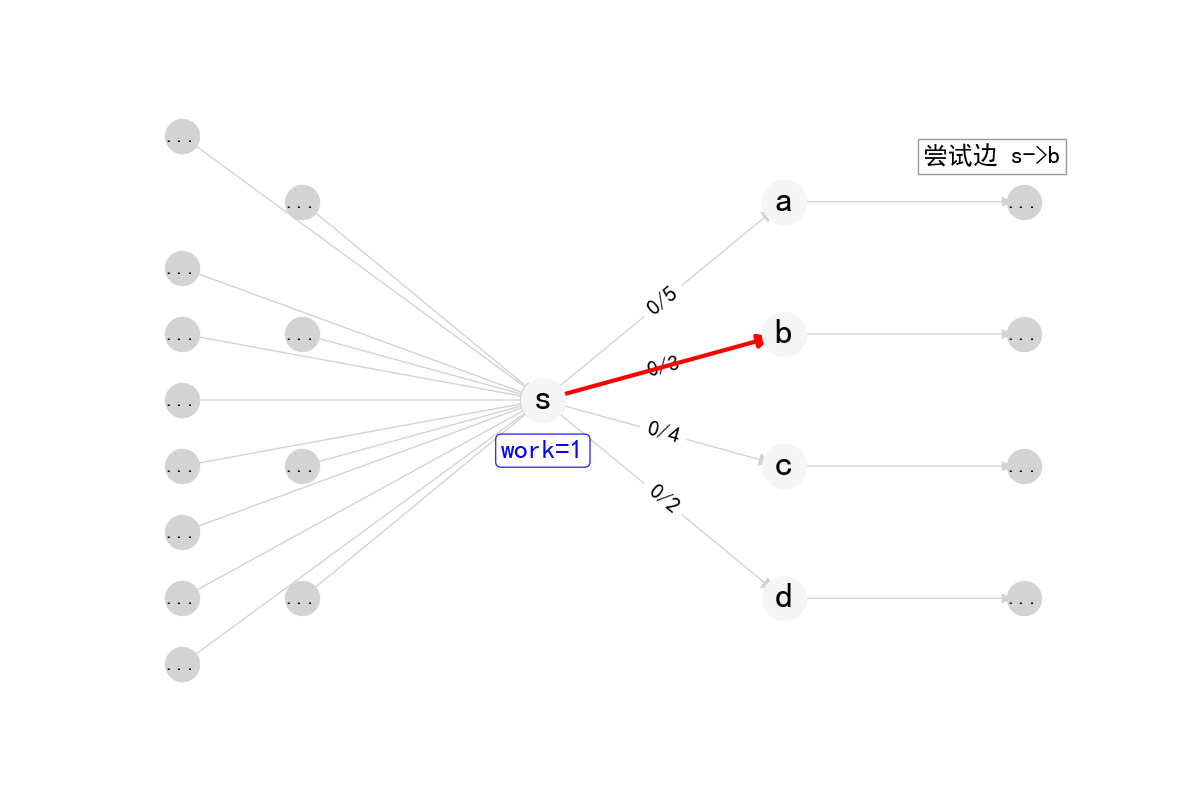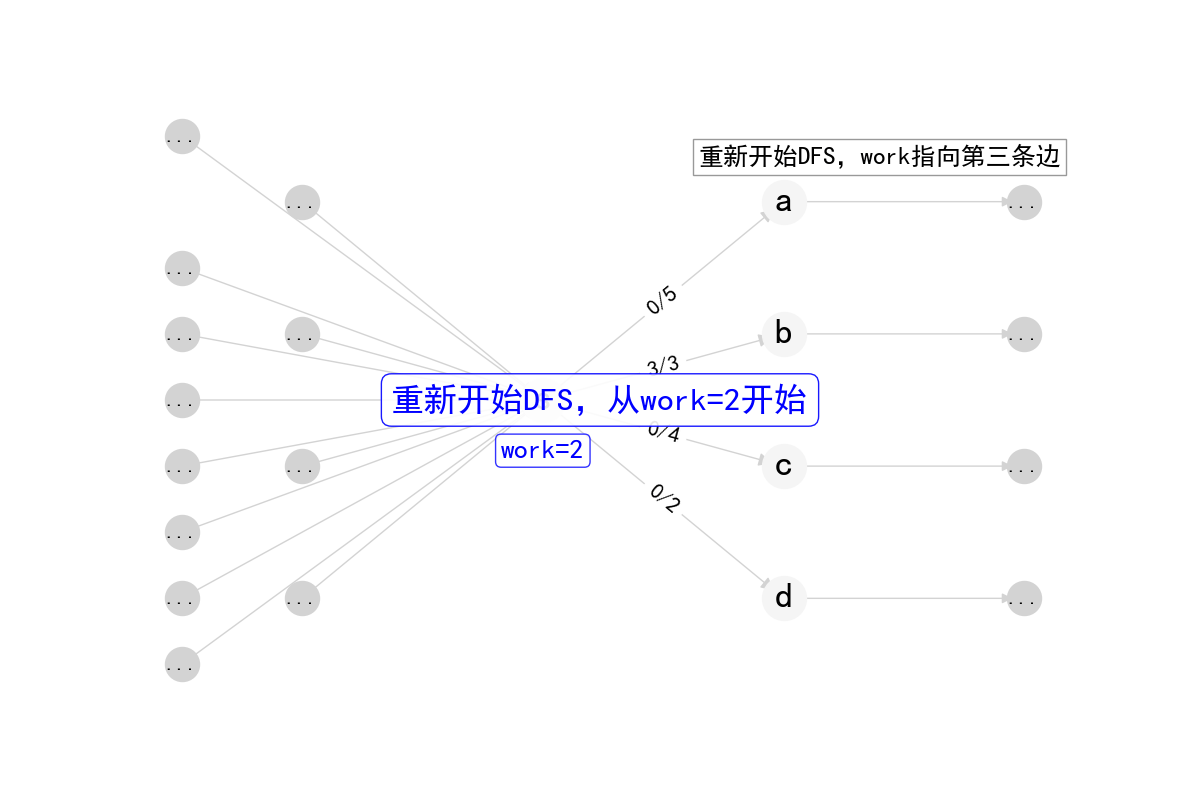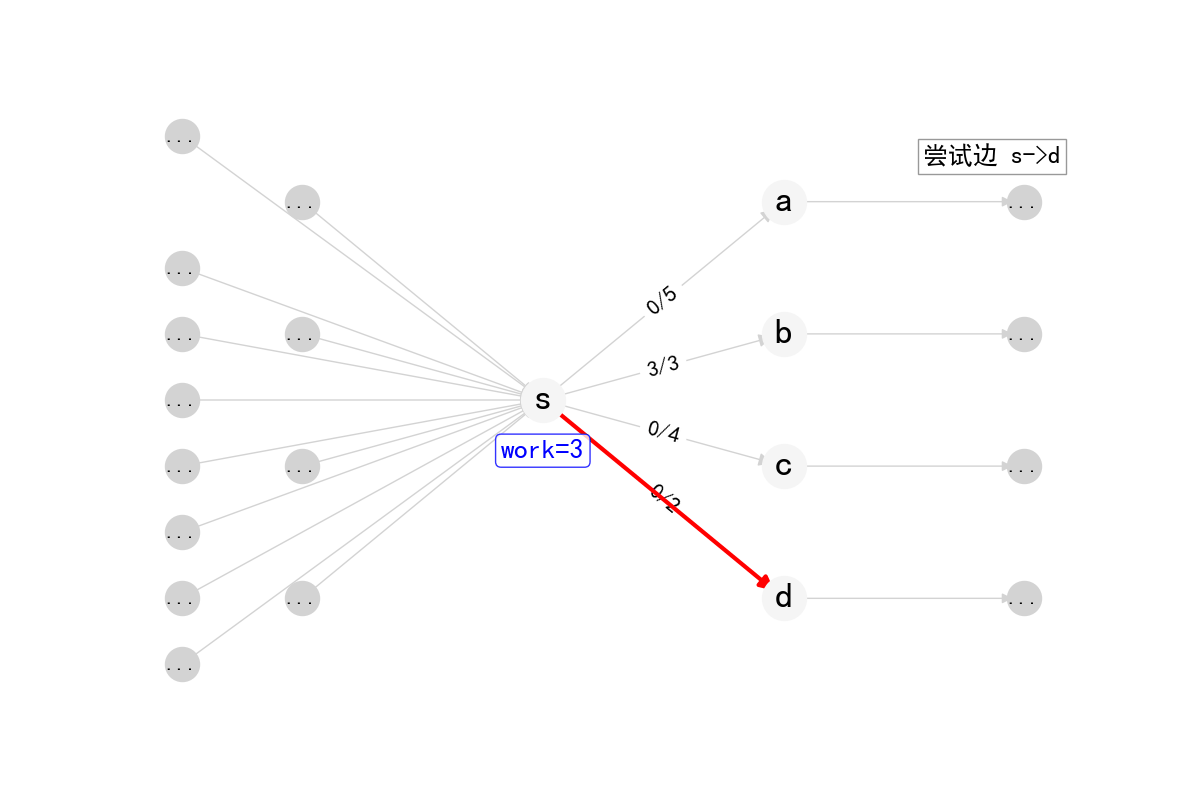
在Dinic算法中，work数组实现了弧优化(arc optimization)，这是一个重要的优化技巧。

work数组记录了每个节点当前遍历到的边的位置。当一条边被证明无法增广时，下次DFS到达这个节点时就不需要从头开始遍历，而是从上次遍历到的位置继续。

  1. 每次BFS建立分层图后，work[i]被初始化为fst[i]，即每个点的第一条边
  2. 在DFS过程中，如果某条边无法增广，work[i]会自动移动到下一条边
  3. 由于分层图中的流量只能沿着层数增加的方向推送，一旦某条边无法增广，在当前分层图中它就永远无法增广了
  4. 因此不需要在下一次DFS时重新检查这条边，直接从work[i]记录的位置继续即可

最大流最小割定理

割(Cut):

将所有点划分为 \(S\) 和 \(V-S\) 两个集合，其中源点 \(s \in S\)，汇点 \(t \in T\)。

割的容量:

  • \(c(S,T)\) 表示从集合 \(S\) 到集合 \(T\) 的所有边的容量之和
  • 也可以用 \(c(s,t)\) 表示 \(c(S,T)\)

最小割(Minimum Cut):

求一个割 \((S,T)\) 使得割的容量 \(c(S,T)\) 最小

最小割与最大流的关系可以这样理解:

想象一个水管系统，从源点 \(s\) 向汇点 \(t\) 输送水，如果要切断水流，必须切断所有从 \(S\) 到 \(T\) 的管道，为了代价最小，我们要找到容量和最小的一组管道切断，这组管道就构成了最小割，而这些管道的容量和，恰好等于系统能输送的最大水流量

最大流最小割定理即： 最大流的值等于最小割的值

例：最小割点

两台电脑通过一系列诸如交换机、路由器等网络设备通信，只要还有网络设备连通它们，就能互相通信，给定它们的相连关系，至少坏掉几个网络设备，会使这两台电脑无法通信？

拆点为边，求最小割集

拆点建图参考

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 设两个设备编号1和2，其余点输入编号 2~n
inline int InP(int x) { return x * 2;}
inline int OutP(int x) { return x * 2 + 1;}
while(m --) {
    scanf("%d%d", &a, &b);  // a、b之间有条边
    // 重新编号，把节点 x 拆成两个点，“入点”编号为 x*2，“出点”编号为 x*2+1
    // a*2+1 作为出点，连一条发往入点 b*2 的边，反之同理
    DbEdge(OutP(a), InP(b), inf);
    DbEdge(OutP(b), InP(a), inf);
}
for(int i = 1; i <= n; i ++) {
    DbEdge(InP(i), OutP(i), 1); // 原始节点的“入点”向“出点”设置容量为 1 的边
}
so = 0; te = (n + 1) * 2;       // 新建源点为0，汇点为 (n+1) * 2，确保与现有编号不冲突
n = (n + 1) * 2 + 1;            // 把节点数 n 改为实际建的点数
DbEdge(so, InP(1), inf); DbEdge(so, OutP(1), inf);  // 用新建的源点把不该拆的设备1的点“短路”
DbEdge(InP(2), te, inf); DbEdge(OutP(2), te, inf);  // 用新建的汇点把不该拆的设备2的点“短路”

为什么这样建图有效：

  • 如果要删除一个节点，就必须切断其入点到出点的边
  • 这条边的容量为\(1\)，表示删除这个节点的代价为\(1\)
  • 其他边的容量为\(inf\)，表示这些边不能被切断
  • 最小割就会选择切断最少的入点-出点边，即删除最少的节点

费用流

费用流是在最大流的基础上，给每条边增加一个费用属性，表示单位流量通过这条边需要付出的代价。

最小费用最大流问题就是在最大流的基础上，要求总费用最小。

负圈

一个图中有负数边，如何求最短路？

——可能没有最短路

如果存在负数圈，路径长度可以无限变小

Floyd 可以判负圈：执行算法求两两最短路，如果一个点到自己的距离为负，则说明有负圈。

最小费用流-负回路算法

在最大流算法的基础上：

  • 在辅助网络上构造新的可行流\(f\)
  • 在\(f\)上寻找费用为负数的圈（用Floyd），由流量守恒知，圈的流量为\(0\)
  • 在原流上不断叠加费用为负的圈，则总流量不变，总费用减少
  • 重复\(1\sim 3\)直到找不到费用为负的圈为止

最小费用流-最短路径算法

不断通过费用最小的增广路增加流

该算法有多种实现形式，这里掌握一个类Dinic的写法

二分图匹配

设有4个申请读研的学生(\(S_i\))与4位导师(\(T_i\))：

每个导师最多只能招收1名学生，每个学生也只能跟随1名导师，下图的边表示学生想要申请的导师

如何分配学生与导师的对应关系，能够满足最多学生的志愿

匈牙利算法

假设我们已经找到了一些学生和导师的配对关系,我们把这些配对关系称为"匹配"。

在所有的连线中:

  • 已经配对的连线称为"匹配边"
  • 还没有配对的连线称为"非匹配边"
  • 已经配对的学生和导师称为"饱和点"

如果我们沿着匹配边和非匹配边交替走,形成的路径就叫"交错路径"。

特别地,如果一条交错路径的起点和终点都是还没有配对的学生或导师(即非饱和点),我们就把这条路径叫做"增广交错路径"。

一个重要的性质:

如果我们找到了一条增广交错路径P,那么可以通过这条路径来增加匹配数:

  • 把路径P上的非匹配边变成匹配边
  • 把路径P上的匹配边变成非匹配边

这样操作后: 1. 得到的新的边集合仍然是一个合法的匹配 2. 新的匹配比原来的匹配多了一条边

这就说明,每找到一条增广交错路径,就能让匹配数增加1。

匈牙利算法的具体步骤如下:

  1. 先随便找一些配对关系作为初始匹配
  2. 重复以下步骤:
    • 寻找一条增广交错路径
    • 如果找到了,就沿着这条路径,把匹配边变成非匹配边,非匹配边变成匹配边
    • 如果找不到增广交错路径了,算法结束
  3. 此时得到的就是最大匹配

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
bool SearchPath(int u) {                // DFS寻找增广交错路线
    for(int v = 1; v <= yN; ++ v) {
        if(g[u][v] && !chk[v]) {        // u->v 有边且 v 尚未搜索
            chk[v] = true;              // 标记搜索
            if(yM[v] == -1 || SearchPath(yM[v])){
                // v 尚未匹配，或者 v 已匹配且沿着 v 的匹配对象找到增广交错路线
                yM[v] = u, xM[u] = v;   // 将 v 与 u 匹配，即执行交错路线的“异或”操作
                return true;            // 表示找到增广交错路线
            }    
        }
    }
    return false;                       // 没找到增广交错路线
}
int Hungarian() {
    memset(xM, -1, sizeof(xM));         // 初始化匹配对象为空
    memset(yM, -1, sizeof(yM));         // 初始化匹配对象为空
    int ret = 0;                        // 初始化匹配数
    for(int u = 1; u <= xN; u ++) {     // 考察 x 这一边的每个点
        if(xM[u] == -1) {               // 如果 u 没有匹配对象，尝试从 u 出发搜索
            memset(chk, false, sizeof(chk));    // 初始化DFS标记
            ret += SearchPath(u);       // 如果找到增广交错路线，则匹配总数 +1
        }
    }
    return ret;
}

二分图最大匹配与最大流

二分图的最大匹配问题可以转化为最大流问题来求解。具体做法是:

  1. 添加一个源点s和汇点t
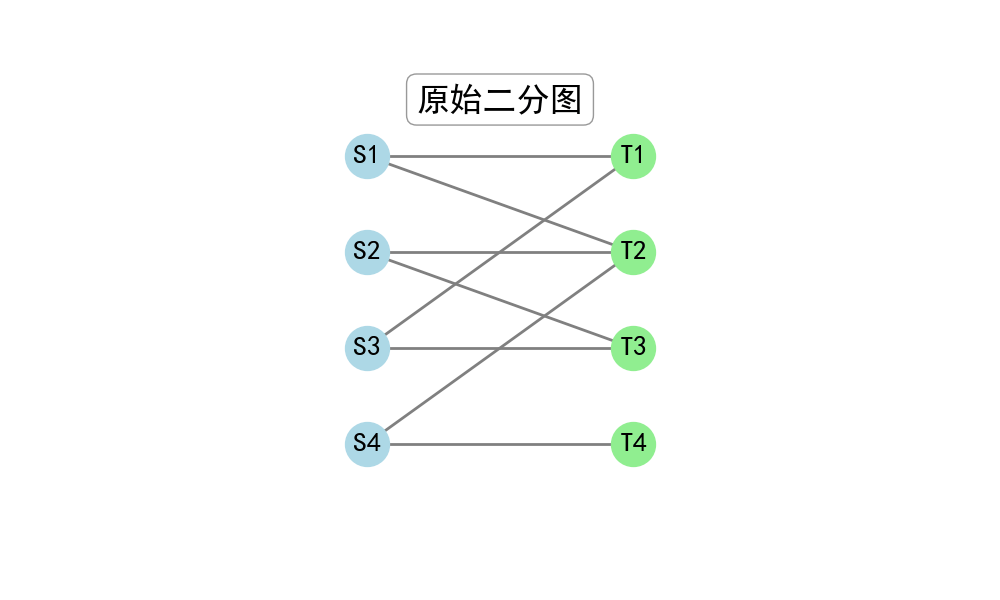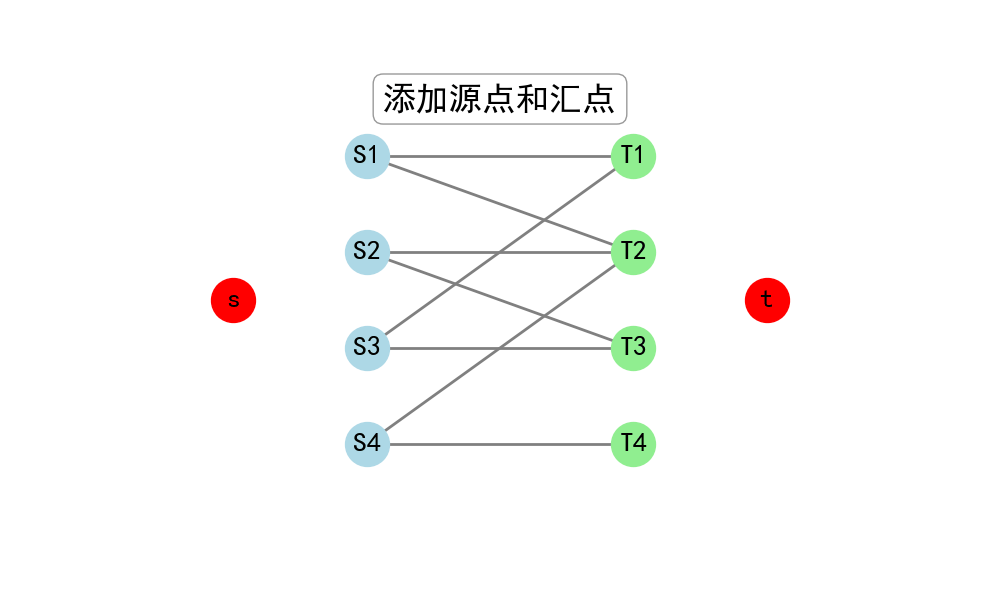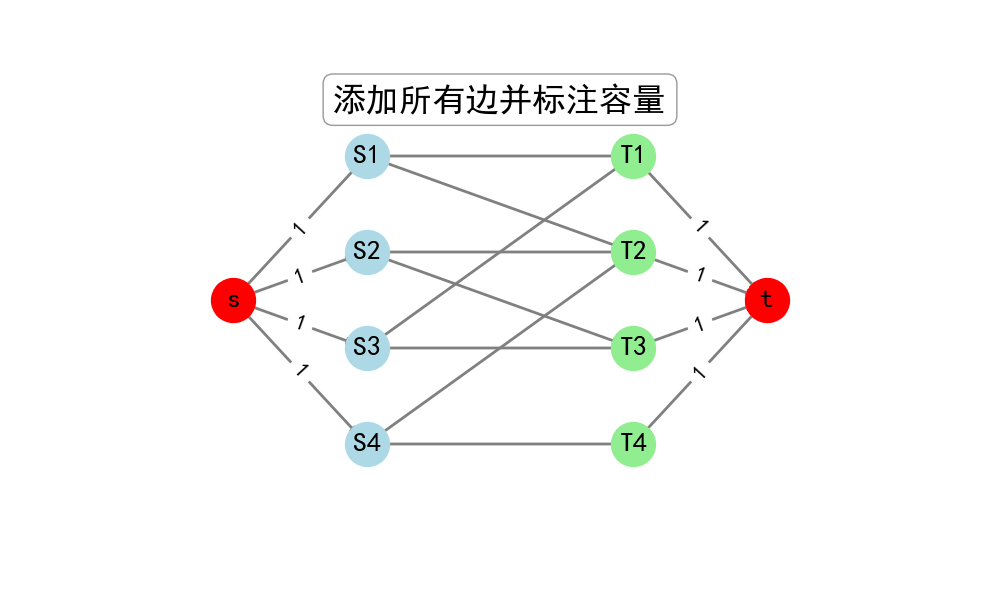
  2. 从源点s向二分图左边所有点连边,容量为1
  3. 从二分图右边所有点向汇点t连边,容量为1
  4. 原二分图中的边改为从左向右的有向边,容量为1

这样构造出的网络流模型中,最大流的值就等于原二分图的最大匹配数。因为:

  • 每条边容量为1,表示每个点最多只能匹配一次
  • 从s到t的一条流量为1的路径,对应了二分图中的一个匹配